Arkus tangens

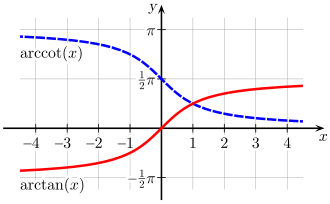
Arkus tangens je jedna z cyklometrických funkcí, inverzní funkce k funkci tangens. Obvykle se značí arctg x nebo arctan x, v anglické literatuře se taktéž používá atan x či tan⁻¹ x. Její hodnotou je úhel v obloukové míře z intervalu ${\displaystyle (-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}})}$, popřípadě ve stupňové míře z intervalu (−90°; 90°), jehož tangens je x. Je to jedna z nejdůležitějších funkcí matematické analýzy.

Definice

Funkce arctg x je inverzní funkce k funkci tg x, jejíž definiční obor byl omezen na interval ${\displaystyle (-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}})}$. Díky tomuto omezení je výchozí funkce prostá, takže požadovaná inverzní funkce existuje.

Vlastnosti

Funkce ${\displaystyle y={\mbox{arctg }}x}$ v obloukové míře je bijekcí mezi množinou reálných čísel ${\displaystyle \mathbb {R} }$ a intervalem ${\displaystyle (-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}})}$, což mimo jiné dokazuje, že každý interval má stejnou mohutnost jako množina reálných čísel.

Dále má tato funkce následující vlastnosti:

Definiční obor	${\displaystyle \mathbb {R} }$
Obor hodnot	${\displaystyle (-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}})}$
Omezenost	Je omezená
Monotonie	Je rostoucí, a tedy prostá
Symetrie	Je lichá
Periodicita	Není periodická
Limity	${\displaystyle \lim _{x\to -\infty }{\mbox{arctg }}x=-{\tfrac {\pi }{2}}}$ ${\displaystyle \lim _{x\to +\infty }{\mbox{arctg }}x={\tfrac {\pi }{2}}}$ ${\displaystyle \lim \limits _{x\rightarrow 0}{{\mbox{arctg }}x \over x}=1,}$  takže v okolí nuly je ${\displaystyle {\mbox{arctg }}x\approx x}$
Inverzní funkce	${\displaystyle x={\mbox{tg }}y}$   (tangens)
Derivace	${\displaystyle {\mathrm {d} \over \mathrm {d} x}\,{\mbox{arctg }}x={1 \over {1+x^{2}}}}$
Integrál	${\displaystyle \int {\mbox{arctg }}x\;\mathrm {d} x=x\;{\mbox{arctg }}x-{\tfrac {1}{2}}\ln(1+x^{2})+C}$

Vzorce

${\displaystyle {\mbox{arctg }}x={\tfrac {\pi }{2}}-{\mbox{arccotg }}x=\arcsin {\frac {x}{\sqrt {x^{2}+1}}}={\tfrac {\pi }{2}}-\arccos {\frac {x}{\sqrt {x^{2}+1}}}}$

${\displaystyle {\mbox{arctg }}(-x)=-{\mbox{arctg }}x}$

${\displaystyle {\mbox{arctg }}{1 \over x}={\begin{cases}{\tfrac {\pi }{2}}-{\mbox{arctg }}x={\mbox{arccotg }}x&{\text{pokud }}x>0\\-{\tfrac {\pi }{2}}-{\mbox{arctg }}x=-\pi +{\mbox{arccotg }}x&{\text{pokud }}x<0\end{cases}}}$

${\displaystyle {\tfrac {1}{2}}\,{\mbox{arctg }}x={\mbox{arctg}}\,{x \over 1+{\sqrt {1+x^{2}}}}}$

${\displaystyle 2\,{\mbox{arctg }}x\equiv {\mbox{arctg}}\,{2x \over 1-x^{2}}{\pmod {\pi }},\quad x\neq \pm 1}$ ^{[p 1]}

${\displaystyle {\mbox{arctg }}x+{\mbox{arctg }}y\equiv {\mbox{arctg}}\,{x+y \over 1-xy}{\pmod {\pi }},\quad xy\neq 1}$

Poznámky

Externí odkazy

• Obrázky, zvuky či videa k tématu arkus tangens na Wikimedia Commons