Identité d'Euler

Ne doit pas être confondue avec l'identité d'Euler du théorème d'Euler (fonctions de plusieurs variables), ni avec les deux identités d'Euler liées au théorème q-binomial.
En mathématiques, l'identité d'Euler est une relation entre plusieurs constantes fondamentales et utilisant les trois opérations arithmétiques d'addition, multiplication et exponentiation :
Elle est nommée d'après le mathématicien Leonhard Euler qui la fait apparaître dans son Introductio, publié à Lausanne en 1748. Avant d'être citée par Euler, cette formule était connue du mathématicien anglais Roger Cotes, mort en 1716.
Démonstration
Par l'analyse complexe
Puisque cos π = –1 et sin π = 0, cette formule est le cas particulier x = π de la formule d'Euler en analyse complexe (pour tout nombre réel x, eix = cos x + i sin x).
C'est aussi le cas particulier n = 2 de la nullité de la somme des racines n-ièmes de l'unité.
Par la géométrie
-
 Juxtaposition de 8 triangles rectangles
Juxtaposition de 8 triangles rectangles -
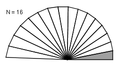 Juxtaposition de 16 triangles rectangles
Juxtaposition de 16 triangles rectangles -
 Illustration du résultat
Illustration du résultat
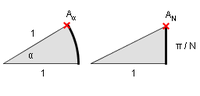
L'interprétation géométrique qui fournit une piste de démonstration par une suite est basée sur la juxtaposition de triangles rectangles.
or, les multiplications complexes se traduisant par des rotations, le point de coordonnées est obtenu en juxtaposant N triangles rectangles[1].
Beauté mathématique
L'identité d'Euler est souvent citée comme un exemple de beauté mathématique[2].
En effet, outre l'égalité, trois des opérations fondamentales de l'arithmétique y sont utilisées, chacune une fois : l'addition, la multiplication et l'exponentiation. L'identité fait également intervenir cinq constantes mathématiques fondamentales[3] :
- 0, l'élément neutre de l'addition.
- 1, l'élément neutre de la multiplication.
- π, omniprésente en trigonométrie, en géométrie dans l'espace euclidien et en analyse mathématique (π = 3,14159265...)
- e, base des logarithmes qui apparait souvent en analyse, calcul différentiel et mathématiques financières (e = 2,718281828...). Tout comme π, c'est un nombre transcendant.
- i, l'unité imaginaire à la base des nombres complexes, qui ont permis l'étude de la résolution des équations polynomiales avant de voir leur usage élargi.
L'inventaire de ces différents éléments est mieux mis en évidence par la notation polonaise inverse de la formule d'Euler :
- 0 ; 1 ; e ; i ;π ; * ; ^ ; +; =
De plus, sous cette forme, l'identité est écrite comme une expression égale à zéro, une pratique courante en mathématique.
On en déduit que l'exponentielle complexe est 2πi-périodique.
Hommages
Paul J. Nahin, professeur émérite de l'université du New Hampshire, écrit dans son ouvrage consacré à l'identité d'Euler et ses applications en analyse de Fourier que la formule définit « l'étalon-or de la beauté mathématique »[4].
Quand l'identité d'Euler fut révélée à Benjamin Peirce, il déclara : « Messieurs, c’est certainement vrai, c’est absolument paradoxal ; on ne peut pas la comprendre, et on ne sait pas ce qu'elle signifie, mais nous l'avons prouvée, et dès lors, nous savons qu'elle doit être la vérité. »[5].
Le célèbre physicien Richard Feynman la considère même comme « la formule la plus remarquable des mathématiques[6] ».
L'identité d'Euler apparaît également dans le roman La Formule préférée du professeur de Yōko Ogawa.
Histoire
Le mathématicien anglais Roger Cotes (mort en 1716, quand Euler avait seulement 9 ans) connaissait cette identité. Euler pourrait en avoir appris l'existence par son compatriote suisse Johann Bernoulli[7].
Notes et références
- ↑ (en) Tristan Needham, Visual Complex Analysis, Oxford, Oxford University Press, , 592 p. (ISBN 0-19-853447-7), p. 82-84.
- ↑ (en) James Gallagher, « Mathematics: Why the brain sees maths as beauty », BBC News online, (lire en ligne).
- ↑ (en) John Allen Paulos, Beyond Numeracy: An Uncommon Dictionary of Mathematics, Penguin, 1992 (ISBN 0-14-014574-5), p. 117.
- ↑ (en) Robert P. Crease (en), « Equations as icons », PhysicsWeb, mars 2007 (accès sur inscription).
- ↑ (en) Eli Maor, e: The Story of a number, Princeton University Press, 1998 (ISBN 978-0-691-14134-3), p. 160 et (en) Edward Kasner et James R. Newman, Mathematics and the Imagination (en), Dover, 2013 (1re éd. Simon & Schuster, 1940), p. 103-104.
- ↑ (en) Richard P. Feynman, Robert B. Leighton et Matthew Sands (en), Feynman Lectures on Physics [détail de l’édition], vol. I, chap. 22, formule 22.9 : « the most remarkable formula in mathematics ».
- ↑ (en) Charles Edward Sandifer, The Early Mathematics of Leonhard Euler, American Mathematical Society, p. 4. (ISBN 978-0521116602)
v · m Nombre e | |
|---|---|
| Applications | |
| Définitions |
|
| Personnes | |
 Arithmétique et théorie des nombres
Arithmétique et théorie des nombres