Perlin噪声

Perlin噪声（Perlin noise，又稱為柏林噪声）指由Ken Perlin发明的自然噪声生成算法^[1]，具有在函数上的连续性，并可在多次调用时给出一致的数值。在电子游戏领域中可以透过使用Perlin噪声生成具连续性的地形；或是在艺术领域中使用Perlin噪声生成图样。由于Perlin本人的失误，Perlin噪声这个名词现在被同时用于指代两种有一定联系的的噪声生成算法。这两种算法都广泛地应用于计算机图形学，因此人们对这两种算法的称呼存在一定误解。下文中的Simplex噪声和分形噪声都曾在严肃学术论文中被单独的称作Perlin噪声。

本文仅讨论灰度图的情况。对于彩色图像的噪声生成，只要将同样的方法分别应用于各个颜色分量上，再加以合成即可。

Simplex噪声

生成噪声最通常的想法是为每个像素赋予一个随机的灰度值。如此产生的图像如下图左。

使用随机方法产生的白噪声
左图的频谱
对随机噪声进行柔化
左图的频谱

用随机法产生的噪声图像和显然自然界物体的随机噪声有很大差别，不够真实。1985年Ken Perlin指出^[1]，一个理想的噪声应该具有以下性质：

对旋转具有统计不变性；
能量在频谱上集中于一个窄带，即：图像是连续的，高频分量受限；
对变换具有统计不变性。

对于计算机图形学中的普遍应用，噪声应该是伪随机的，两次调用应得到同样的结果。

上图的噪声之所以不够真实是因为它的能量在频谱中平均分布，即它是白噪声。对白噪声进行柔化处理后限制了噪声的频谱，比之前者和自然界中的噪声现象更加接近，但是依然不能令人满意。

经典Perlin噪声

Perlin在上述文章中提出了一种产生符合要求的一维噪声函数的简单方法，这是后续工作的基础：

在一维坐标轴上，选择等距的无穷个点，将值空间划分为等长的线段（为方便起见，选择坐标值为整数的点），为每个点随机指定一个值^{[來源請求]}；
对于坐标值为整数的点，将该点对应的值作为噪声图像上该点的值；对于坐标值不为整数的点，将相邻两点的值进行插值运算，获得该点的数值(灰度)。

插值使用的函数是一个在0处为1，在1处为0，在0.5处为0.5的连续单调减函数。例如，设 $c_{0},c_{1}$ 为左右两整数点的数值， $t$ 为该点距离左边点的距离，使用 $(1-t)$ 作为插值函数，则该点的值为 $c_{1}(1-t)+c_{0}t$ 。

$(1-t)$ 是线性插值，得到的结果人工痕迹严重，且在整数点上不连续。Perlin建议使用 $3t^{2}-2t^{3}$ 作为插值函数 ^[1]，后来又建议使用 $6t^{5}-15t^{4}+10t^{3}$ 作为插值函数^[2]；事实上，只要是在区间[0,1]内连续的函数 $f$ ，有 $f(0)=1$ ， $f(1)=0$ 且 $f'(0)=f'(1)=0$ 的函数皆可做为插值函数。实际应用如下：设 $f$ 为插值函数，插值结果为 $c_{0}f(1-t)+c_{1}f(t)$ 。

对于二维的情况，可以将上述算法进行推广，即：

为所有坐标为 $(x,y)$ 且 $x,y$ 都是整数的点指定一个值，同时指定一个梯度，这些点将空间分成方格；
对于坐标轴为整数的点，即上述方格的顶点，将为它指定的值作为该点的值；对于某个方格内部的点 $(x,y)$ ，用所在方格四个顶点的值和梯度进行插值。

例如，对于点 $(x,y)$ ，令 $i=\lfloor x\rfloor ,j=\lfloor y\rfloor$ 它所在方格的四个顶点分别为： $(i,j)$ 、 $(i+1,j)$ 、 $(i+1,j+1)$ 、 $(i,j+1)$ 。令 $u=x-i,v=y-j$ ，这四个顶点对点 $(x,y)$ 的贡献可以用它们的梯度（ $g_{00},g_{10},g_{11},g_{01}$ ）和 $(x,y)$ 点与这四个顶点的方向（ $(u,v)$ 、 $(u-1,v)$ 、 $(u-1,v-1)$ 、 $(u,v-1)$ ）进行点积获得。但是在二维的情况下，插值更为复杂。首先需要对 $(i,j)$ 和 $(i+1,j)$ 两点在 $x$ 方向插值，得到点 $(x,j)$ 的值；之后对 $(i,j+1)$ 和 $(i+1,j+1)$ 两点在x方向插值，得到点 $(x,j+1)$ 的值；最后对 $(x,j)$ 和 $(x,j+1)$ 在 y 方向插值，得到 $(x,y)$ 的值。

在三维的情况下，需要进行七次插值。可以证明，插值次数随着维数的增长指数增长。

经典Perlin噪声基本满足Perlin提出的噪声条件。但是由于 $3t^{2}-2t^{3}$ 导数中含有线性分量，在计算相邻点差时会体现出人工效果，不够自然。经典Perlin噪声在进行下文的分形和运算后效果不够自然^[2]。

经典Perlin噪声的软件实现

为了达到伪随机性，经典Perlin噪声（和随后的Simplex噪声）通过在一个转置数组中查询点的坐标求每个点的梯度，而不使用随机数发生器。这样两次调用可以获得同样的结果，达到伪随机性。理论上转置数组可以任意指定，但是后续的实现都使用Perlin最初提出的数组：

unsigned char perm[256] = {151,160,137,91,90,15,
  131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
  190,6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
  88,237,149,56,87,174,20,125,136,171,168,68,175,74,165,71,134,139,48,27,166,
  77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
  102,143,54,65,25,63,161,1,216,80,73,209,76,132,187,208,89,18,169,200,196,
  135,130,116,188,159,86,164,100,109,198,173,186,3,64,52,217,226,250,124,123,
  5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
  223,183,170,213,119,248,152,2,44,154,163,70,221,153,101,155,167,43,172,9,
  129,22,39,253,19,98,108,110,79,113,224,232,178,185,112,104,218,246,97,228,
  251,34,242,193,238,210,144,12,191,179,162,241,81,51,145,235,249,14,239,107,
  49,192,214,31,181,199,106,157,184,84,204,176,115,121,50,45,127,4,150,254,
  138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180};

以下用python示例如何生成一维Perlin噪声，更高维的情形可以在这个基础去推广：

from math import floor

#Perlin 最初提出的数组
SEQ = [
  151,160,137,91,90,15,
  131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
  190,6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
  88,237,149,56,87,174,20,125,136,171,168,68,175,74,165,71,134,139,48,27,166,
  77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
  102,143,54,65,25,63,161,1,216,80,73,209,76,132,187,208,89,18,169,200,196,
  135,130,116,188,159,86,164,100,109,198,173,186,3,64,52,217,226,250,124,123,
  5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
  223,183,170,213,119,248,152,2,44,154,163,70,221,153,101,155,167,43,172,9,
  129,22,39,253,19,98,108,110,79,113,224,232,178,185,112,104,218,246,97,228,
  251,34,242,193,238,210,144,12,191,179,162,241,81,51,145,235,249,14,239,107,
  49,192,214,31,181,199,106,157,184,84,204,176,115,121,50,45,127,4,150,254,
  138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180]

#插值函数
def _blending(t):
    return t*(t*(t*(10+t*(-15+6*t))))              #6t^5 -15t^4 + 10t^3

def noise(pos):
    if pos%1 == 0:                                 #对于整数点，直接从数列中取得数值即可。
        return SEQ[int(pos%255)]
    else:                                          #对于非整数的点，由左右的整数进行插值运算得出数值。
        x0,x1 = floor(pos)%255,floor(pos+1)%255    #取得非整数点旁的两个整数。
        c0,c1 = SEQ[x0],SEQ[x1]                    #从数列中取得两个整数点的数值。
        t = pos%255 - x0                           #计算非整数点离左边整数点的距离。
        return (c0*_blending(1-t)+c1*_blending(t)) #使用插值函数计算非整数点的数值并输出。

使用以上示例中的noise()函数便可生成Perlin噪声。

在生成梯度时，理论上应该任意生成一个长度为1的向量。在实现中，一维的情况下可以在 $8,7,6,5,4,3,2,1,-1,-2,-3,-4,-5,-6,-7,-8$ 这16个整数中任选一个作为斜率，这样可以方便的通过对坐标值进行位操作实现。二维的情况下，梯度可以从 $(1,2),(2,1),(-1,2),(-2,1),(-1,-2),(-2,-1),(1,-2),(2,-1)$ 这8个向量之中随机选择一个。这8个向量具有相同的长度，因此点积后的归一化计算可以省略。三维的情况下，梯度可以从以原点为中心，边长为2的正方体每边的中点共12个向量中选择，即从 $(0,1,1),(0,1,-1),(0,-1,-1),(0,-1,1),(1,0,1),(1,0,-1),(-1,0,-1),(-1,0,1),(1,1,0),(-1,1,0),(-1,-1,0),(1,-1,0)$ 中选择一个。在实际实现时也可以通过位操作进行。^[3]

Simplex噪声

使用Simplex方法产生噪声
左图的频谱

为了简化计算，方便使用硬件实现，Ken Perlin在2002年对他的方法进行了改进，改进的方法称为 Simplex 噪声。Simplex 噪声使用 $6t^{5}-15t^{4}+10t^{3}$ 作为插值函数，杜绝了导数中的线性部分。另外，Simplex 噪声算法有效地降低了插值次数。

如上文，二维经典Perlin噪声将二维空间用正方形填充，用四个顶点进行3次插值，而Simplex噪声将二维空间用等边三角形填充，使用三个顶点进行插值。三维经典Perlin噪声将三维空间用立方体进行填充，使用8个顶点进行7次插值，三维Simplex噪声使用正四面体填充空间，用4个顶点进行插值。对于更高维（N维）的情况，经典Perlin噪声将空间用超立方体填充，顶点数目是 $2^{N}$ ，而Simplex噪声使用高维正三角形（称为Simplex）进行填充，顶点数目为 $N+1$ 。Simplex噪声插值次数随维数增长线性增长。

对于二维的情况，使用正三角形填充空间使得直接判断某点落在哪个正三角形中，计算该三角形的顶点位置变得复杂。在实现上通常通过坐标变换将正三角形映射成直角三角形。使用该方法进行变换可以使用和经典Perlin噪声相同的方法对顶点进行求值^[3]。

Simplex噪声和经典Perlin噪声的应用

Perlin噪声可以用来模拟自然界中的噪声现象。由于它的连续性，如果将二维噪声中的一个轴作为时间轴，得到的就是一个连续变化的一维函数。同样的也可以得到连续变化的二维图像。该噪声可以用来模拟人体的随机运动，蚂蚁行进的线路等。另外，还可以通过计算分形和模拟云朵，火焰等非常复杂的纹理。^[3]。

Perlin噪声对各个点的计算是相互独立的，因此非常适合使用图形处理器进行计算。OpenGL在GLSL中定义了一维至四维的噪声函数noise1、noise2、noise3、noise4，在该规范中噪声的性质与上述Perlin提出的性质相同。在Mesa 3D实现中，这一组函数是使用Simplex算法实现的。在硬件的实现中，噪声的生成可以达到实时效果。

分形噪声

分形噪声是上述Perlin 1985年的文章中提出的将符合上文所述三条件的噪声通过计算分形和构造更复杂效果的算法。

分形噪声可以用来模拟自然界的自相似过程，包括海岸线，地形，海浪等。分形噪声的原理是利用Perlin噪声频率受限的特性，通过不断叠加更高频率的Perlin噪声达到自相似的效果。

一维分形噪声

在一维的情况下，设噪声函数为 $noise(x)$ ，则通过 $noise(2x),noise(4x)$ 等就可以构造更高频率的噪声。

下图左边是一维Perlin噪声频率频率在不断倍增，振幅不断倍减的情况，右图是左边这些函数求和的图像。

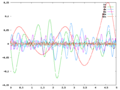6条频率倍增的一维Perlin噪声
一维Perlin噪声分形和右边的图像是自相似的，将它放大会得到和原图相似的效果。

从数学上描述分形噪声，则是：

$\sum _{t}{\frac {Noise(2^{i}point)}{2^{i}}}$

分形噪声有时也被称作 $1/f$ 噪声^[1]。

二维分形噪声

对于二维的情况，可以使用类似的方法进行分形和运算，产生的效果类似于云层，如下图所示。

二维Simplex噪声原函数
二维Simplex噪声叠加2倍频
二维Simplex噪声叠加到4倍频
二维Simplex噪声叠加到128倍频

对分形和函数进行一些小修改可以模拟各种复杂效果。

描述	結果
$\sum _{t}{\frac {\left\|Noise(2^{i}point)\right\|}{2^{i}}}$
$\sin(x+\sum _{t}{+{\frac {\left\|Noise(2^{i}point)\right\|}{2^{i}}}})$

同上，将三维分形噪声中的一个轴作为时间轴，可以构造连续动态的噪声效果。

参考文献

^ ^1.0 ^1.1 ^1.2 ^1.3 Ken Perlin. An image synthesizer. SIGGRAPH Comput. Graph. 1985, 19: 287––296. ISSN 0097-8930.
^ ^2.0 ^2.1 Ken Perlin. Improving noise. ACM. 2002: 681––682. ISBN 1-58113-521-1. |booktitle=被忽略 (帮助)
^ ^3.0 ^3.1 ^3.2 Stefan Gustavson. Simplex noise demystified (PDF). 2005-03-22 [2008-09-17]. （原始内容存档 (PDF)于2008-12-09）.
^ Perlin Noise. [2008-09-17]. （原始内容存档于2008-07-24）.

外部链接

An image synthesizer Ken Perlin在1985年研究像素渲染器时提出了噪声的性质
Noise Hardware（页面存档备份，存于互联网档案馆） Ken Perlin在2002年研究用硬件发生噪声时改进了原有的噪声生成算法，新算法称为Simplex噪声
Simplex noise demystified（页面存档备份，存于互联网档案馆）对Simplex noise进行详细的介绍
Implementing Improved Perlin Noise Ken Perlin为NVIDIA GPU Gems第一版撰写了一篇关于Perlin噪声的短文
Implementing Improved Perlin Noise NVIDIA GPU Gems第二版中给出的使用Cg生成Perlin噪声的程序
Perlin Noise关于一维Perlin噪声和分形噪声的简单介绍
Ken Perlin的主页（页面存档备份，存于互联网档案馆）