Bao lồi

Trong hình học, bao lồi của một hình là tập hợp lồi nhỏ nhất chứa hình đó. Bao lồi có thể được định nghĩa là giao của tất cả tập lồi chứa một tập con cho trước của một không gian Euclid, hoặc là tập hợp gồm tất cả tổ hợp lồi của các điểm trong tập con đó. Đối với một tập con bị chặn của mặt phẳng, bao lồi có thể được minh họa thành một hình bao bởi một dây đàn hồi kéo dãn xung quanh tập con đó.

Bao lồi của tập mở là bao lồi mở, và bao lồi của tập compact là bao lồi compact. Mỗi tập lồi compact đều là bao lồi của các điểm cực biên của nó. Toán tử bao lồi là một ví dụ về toán tử đóng, và một antimatroid có thể được biểu diễn bằng cách áp dụng toán tử đóng này cho tập hợp hữu hạn các điểm. Các bài toán thuật toán về việc tìm bao lồi của một tập hợp hữu hạn các điểm trong mặt phẳng hoặc các không gian Euclid ít chiều khác và bài toán đối ngẫu về các nửa không gian giao nhau đều là những vấn đề cơ bản của hình học tính toán. Chúng có thể được giải trong thời gian ${\displaystyle O(n\log n)}$ đối với tập hợp điểm hai chiều hoặc ba chiều, và trong thời gian bằng với độ phức tạp thời gian trong trường hợp tệ nhất được cho bởi định lý cận trên ở không gian nhiều chiều hơn.

Cùng với tập hợp điểm hữu hạn, bao lồi cũng đã được nghiên cứu đối với đa giác đơn, chuyển động Brown, đường cong ghềnh và trên đồ thị của hàm. Bao lồi được ứng dụng rộng rãi trong toán học, thống kê, tối ưu hóa tổ hợp, kinh tế, mô hình hóa hình học và tập tính học. Một số cấu trúc liên quan đến nó bao gồm bao lồi trực giao, lớp lồi, chỏm lồi, tam giác đạc Delaunay và sơ đồ Voronoi.

Định nghĩa

Một tập hợp các điểm trên một không gian Euclid được gọi là tập lồi nếu nó chứa các đoạn thẳng nối từng cặp điểm của nó. Bao lồi của một tập ${\displaystyle X}$ cho trước có thể được định nghĩa là^[1]

1. Tập lồi nhỏ nhất chứa ${\displaystyle X}$
2. Giao của tất cả các tập lồi chứa ${\displaystyle X}$
3. Tập hợp tất cả tổ hợp lồi của các điểm trong ${\displaystyle X}$
4. Hợp của tất cả đơn hình với các đỉnh thuộc ${\displaystyle X}$.

Với tập bị chặn trong mặt phẳng Euclid mà các điểm trong tập đó không tạo thành đường thẳng thì đường biên của bao lồi là đường cong Jordan với chu vi nhỏ nhất chứa ${\displaystyle X}$. Có thể tưởng tượng rằng ta kéo dãn một dây đàn hồi để nó bao quanh toàn bộ tập ${\displaystyle S}$ rồi thả dây ra để nó co lại đến mức tối đa; khi đó, dây bao lại tập lồi của ${\displaystyle S}$.^[2] Cách hiểu này không thể mở rộng được ngay cho không gian nhiều chiều hơn: với một tập hợp hữu hạn các điểm trong không gian ba chiều, một lân cận của một cây bao trùm của các điểm này bao lại chúng với diện tích bề mặt nhỏ tùy ý và nhỏ hơn diện tích bề mặt của bao lồi.^[3] Tuy nhiên, trong không gian nhiều chiều, một số dạng của bài toán vật cản về việc tìm một bề mặt năng lượng thấp nhất nằm trên một hình cho trước có thể có bao lồi là nghiệm của chúng.^[4]

Với các đối tượng trong không gian ba chiều, định nghĩa đầu tiên phát biểu rằng bao lồi là vùng giới hạn lồi nhỏ nhất của các đối tượng đó. Định nghĩa qua giao của các tập lồi có thể được mở rộng cho hình học phi Euclid, và định nghĩa qua tổ hợp lồi có thể được mở rộng từ không gian Euclid sang không gian vectơ thực hoặc không gian afin bất kỳ; bao lồi cũng có thể được khái quát hóa theo một cách trừu tượng hơn sang matroid định hướng.^[5]

Quan hệ giữa các định nghĩa

Định nghĩa đầu tiên không hiển nhiên đúng: vì sao phải tồn tại một tập lồi nhỏ nhất chứa ${\displaystyle X}$ với mọi ${\displaystyle X}$? Tuy nhiên, định nghĩa thứ hai (giao của tất cả các tập lồi chứa ${\displaystyle X}$) lại mang tính rạch ròi hơn. Theo đó, bao lồi là tập con của mỗi tập lồi ${\displaystyle Y}$ khác ${\displaystyle X}$ chứa ${\displaystyle X}$, vì ${\displaystyle Y}$ có trong các tập được giao. Do đó, nó chính là tập lồi nhỏ nhất chứa ${\displaystyle X}$. Vì vậy, hai định nghĩa đầu tiên là tương đương nhau.^[1]

Mỗi tập lồi chứa ${\displaystyle X}$ phải chứa tất cả tổ hợp lồi của các điểm trong ${\displaystyle X}$ (theo giả thiết rằng nó là tập lồi), nên tập hợp tất cả các tổ hợp lồi này có trong giao của tất cả các tập lồi chứa ${\displaystyle X}$. Ngược lại, tập hợp tất cả các tổ hợp lồi cũng là một tập lồi chứa ${\displaystyle X}$ nên nó cũng chứa giao của tất cả các tập lồi chứa ${\displaystyle X}$, và do đó định nghĩa thứ hai và thứ ba là hai định nghĩa tương đương.^[6]

Thực tế, theo định lý Carathéodory, nếu ${\displaystyle X}$ là tập con của một không gian Euclid ${\displaystyle d}$ chiều, mỗi tổ hợp lồi của một số hữu hạn các điểm trong ${\displaystyle X}$ cũng là một tổ hợp lồi của nhiều nhất ${\displaystyle d+1}$ điểm trong ${\displaystyle X}$. Tập hợp các tổ hợp lồi của một bộ gồm ${\displaystyle d+1}$ điểm là một đơn hình; trong mặt phẳng nó là một tam giác và trong không gian ba chiều nó là một tứ diện. Vì vậy, mỗi tổ hợp lồi của các điểm trong ${\displaystyle X}$ đều thuộc một đơn hình có các đỉnh thuộc ${\displaystyle X}$, nên định nghĩa thứ ba và thứ tư là hai định nghĩa tương đương.^[6]

Bao trên và bao dưới

Ở hai chiều, bao lồi đôi khi được chia thành hai phần là bao trên và bao dưới, kéo dài giữa các điểm ngoài cùng bên trái và bên phải của bao đó. Tổng quát hơn, đối với bao lồi trong bất kỳ không gian nhiều chiều nào, có thể chia đường biên của bao đó thành các điểm mặt trên (những điểm mà theo đó một tia hướng lên không giao với bao), điểm mặt dưới và điểm cực biên. Với bao ba chiều, các phần mặt trên và mặt dưới của đường biên tạo thành những đĩa tôpô.^[7]

Tính chất tôpô

Bao đóng và bao mở

Bao lồi đóng của một tập hợp là tập đóng của bao lồi, và bao lồi mở là phần trong (hoặc, trong một số tài liệu, phần trong tương đối) của bao lồi.^[8]

Bao lồi đóng của ${\displaystyle X}$ là giao của tất cả các nửa không gian đóng chứa ${\displaystyle X}$. Nếu bao lồi của ${\displaystyle X}$ đã là một tập đóng (xảy ra chẳng hạn khi ${\displaystyle X}$ là một tập hữu hạn hoặc, tổng quát hơn, là một tập compact) thì nó bằng bao lồi đóng đó. Tuy nhiên, giao của các nửa không gian đóng là tập đóng, nên khi một bao lồi không phải là bao lồi đóng thì nó không thể biểu diễn được theo cách này.^[9]

Nếu bao lồi mở của một tập hợp ${\displaystyle X}$ là bao lồi ${\displaystyle d}$ chiều thì mỗi điểm trong bao đó thuộc một bao lồi mở gồm nhiều nhất ${\displaystyle 2d}$ điểm thuộc tập ${\displaystyle X}$. Tập hợp các đỉnh của một hình vuông, khối bát diện đều, hoặc khối đa diện chéo trong không gian nhiều chiều là những ví dụ về trường hợp cần đúng ${\displaystyle 2d}$ điểm.^[10]

Sự bảo toàn tính chất tôpô

Về mặt tôpô, bao lồi của một tập mở luôn luôn là bao lồi mở, và bao lồi của một tập compact luôn luôn là bao lồi compact. Tuy nhiên, có một số tập đóng có bao lồi không phải là bao lồi đóng.^[11] Chẳng hạn, tập đóng

${\displaystyle \left\{(x,y)\mathop {\bigg |} y\geq {\frac {1}{1+x^{2}}}\right\}}$

(tập hợp các điểm thuộc hoặc nằm phía trên đường cong phù thủy Agnesi) có bao lồi là nửa mặt phẳng trên mở.^[12]

Tính compact của bao lồi của tập compact trong không gian Euclid với số chiều hữu hạn được khái quát hóa bằng định lý Krein–Smulian, theo đó bao lồi đóng của một tập con compact yếu trong một không gian Banach (một tập con có tính compact dưới dạng tôpô yếu) là bao lồi compact yếu.^[13]

Điểm cực biên

Một điểm cực biên của một tập lồi là một điểm trong tập hợp không nằm trên một đoạn thẳng giữa hai điểm khác trong cùng tập hợp đó. Đối với một bao lồi, mỗi điểm cực biên đều phải thuộc tập đã cho, vì ngược lại nó không thể tạo thành một tổ hợp lồi gồm các điểm đã cho. Theo định lý Krein–Milman, mỗi tập lồi compact trong một không gian Euclid (hoặc, tổng quát hơn, trong một không gian vectơ tôpô lồi địa phương) là bao lồi của các điểm cực biên của nó.^[14] Tuy nhiên, định lý này có thể không đúng đối với các tập lồi không compact; ví dụ, toàn bộ mặt phẳng Euclid và quả cầu đơn vị mở đều có tính lồi, nhưng chúng không có điểm cực biên nào. Lý thuyết Choquet mở rộng định lý này từ tổ hợp lồi hữu hạn của các điểm cực biên sang tổ hợp vô hạn trong các không gian tổng quát hơn.^[15]

Tính chất hình học và đại số

Toán tử đóng

Toán tử bao lồi có các tính chất đặc trưng của một toán tử đóng:^[16]

• Bao lồi của một tập ${\displaystyle X}$ bất kỳ là một tập cha của ${\displaystyle X}$.
• Với hai tập hợp ${\displaystyle X}$ và ${\displaystyle Y}$ sao cho ${\displaystyle X\subseteq Y}$ thì bao lồi của ${\displaystyle X}$ là tập con của bao lồi của ${\displaystyle Y}$.
• Với mọi tập hợp ${\displaystyle X}$, bao lồi của bao lồi của ${\displaystyle X}$ bằng bao lồi của ${\displaystyle X}$.

Khi được áp dụng cho một tập hợp hữu hạn các điểm, đó chính là toán tử đóng của một antimatroid, cụ thể là antimatroid bao của tập hợp đó. Mỗi antimatroid đều có thể được biểu diễn theo cách này bằng bao lồi của các điểm trong một không gian Euclid với số chiều đủ lớn.^[17]

Tổng Minkowski

Các phép toán dựng bao lồi và tính tổng Minkowski giao hoán lẫn nhau vì tổng Minkowski của bao lồi của các tập hợp có cùng kết quả với bao lồi của tổng Minkowski của các tập hợp đó. Kết luận này là một bước để chứng minh định lý Shapley–Folkman giới hạn khoảng cách giữa một tổng Minkowski và bao lồi của nó.^[18]

Đối ngẫu xạ ảnh

Phép đối ngẫu xạ ảnh để dựng bao lồi của một tập hợp hữu hạn các điểm chính là phép dựng giao của một họ gồm các nửa không gian đóng chứa điểm gốc (hoặc một điểm bất kỳ xác định).^[19]

Trường hợp đặc biệt

Tập hợp điểm hữu hạn

Bao lồi của một tập hợp điểm hữu hạn ${\displaystyle S\subset \mathbb {R} ^{d}}$ tạo thành một đa giác lồi khi ${\displaystyle d=2}$, hoặc tổng quát hơn là một đa diện lồi trong ${\displaystyle \mathbb {R} ^{d}}$. Mỗi điểm cực biên của bao đó được gọi là đỉnh, và (theo định lý Krein–Milman) mỗi đa diện lồi đều là bao lồi của các đỉnh của nó. Nó chính là đa diện lồi duy nhất có các đỉnh thuộc ${\displaystyle S}$ và bao hết toàn bộ ${\displaystyle S}$.^[2] Với tập hợp các điểm ở vị trí tổng quát, bao lồi là một đa diện đơn hình.^[20]

Theo định lý cận trên, số mặt của bao lồi của ${\displaystyle n}$ điểm trong không gian Euclid ${\displaystyle d}$ chiều là ${\displaystyle O(n^{\lfloor d/2\rfloor })}$.^[21] Đặc biệt, ở hai chiều và ba chiều, số mặt lớn nhất của bao lồi tuyến tính theo ${\displaystyle n}$.^[22]

Đa giác đơn

Bao lồi của một đa giác đơn bao quanh đa giác đã cho và được nó chia thành nhiều vùng, trong đó có một vùng là chính đa giác đó. Các vùng còn lại, giới hạn bởi một chuỗi đa giác của đa giác và một cạnh của bao lồi, được gọi là rãnh (pocket). Thực hiện lặp lại phân tích này với mỗi rãnh một cách đệ quy thì một biểu diễn phân cấp của đa giác đã cho được tạo thành và được gọi là cây sai phân lồi (convex differences tree) của đa giác đó.^[23] Chiếu lại một rãnh qua cạnh bao lồi của nó làm mở rộng đa giác đơn này thành một đa giác mới với chu vi không đổi và diện tích lớn hơn, và định lý Erdős–Nagy phát biểu rằng quá trình mở rộng này sẽ chấm dứt sau một số hữu hạn bước.^[24]

Chuyển động Brown

Đường cong do chuyển động Brown tạo ra trong mặt phẳng, tại bất kỳ thời điểm cố định nào, có xác suất là 1 để có bao lồi mà đường biên tạo thành một đường cong khả vi liên tục. Tuy nhiên, với một góc ${\displaystyle \phi }$ thỏa mãn ${\displaystyle \pi /2<\phi <\pi }$, sẽ có những thời điểm trong chuyển động Brown mà trong đó một chất điểm chạm vào đường biên của bao lồi tại một đỉnh của góc ${\displaystyle \phi }$. Số chiều Hausdorff của tập hợp những thời điểm đặc biệt như thế là ${\displaystyle 1-\pi /2\phi }$ (với xác suất cao).^[25]

Đường cong trong không gian

Đối với bao lồi của một đường cong trong không gian hoặc một tập hợp hữu hạn các đường cong không gian ở vị trí tổng quát trong không gian ba chiều, các phần của đường biên cách ra khỏi những đường cong này là các bề mặt xiên và khai triển được.^[26] Một số ví dụ bao gồm oloid, bao lồi của hai đường tròn trong các mặt phẳng vuông góc, trong đó mỗi đường tròn đều đi qua tâm của đường tròn còn lại;^[27] sphericon, bao lồi của hai nửa đường tròn đồng tâm trong các mặt phẳng vuông góc; và D-form, các hình lồi có được từ định lý Alexandrov đối với một mặt phẳng được tạo thành bằng cách dán hai tập lồi phẳng cùng chu vi lại với nhau.^[28]

Hàm toán học

Bao lồi hoặc bao lồi dưới của một hàm ${\displaystyle f}$ trong một không gian vectơ thực là hàm có trên đồ thị là bao lồi dưới của trên đồ thị của ${\displaystyle f}$. Nó là hàm lồi cực đại duy nhất bị chặn trên bởi ${\displaystyle f}$.^[29] Định nghĩa này có thể được mở rộng cho bao lồi của một tập hợp các hàm (có được từ bao lồi của hợp của các trên đồ thị, hoặc từ giá trị nhỏ nhất theo từng điểm của chúng) và, ở dạng này, có tính đối ngẫu với phép toán liên hợp lồi.^[30]

Tính toán

Trong hình học tính toán, có một số thuật toán để tính bao lồi của một tập hợp hữu hạn các điểm và các đối tượng hình học khác. Ở đây "tính bao lồi" có nghĩa là xây dựng một cấu trúc dữ liệu rõ ràng và hiệu quả để biểu diễn hình lồi cần tìm. Các dạng biểu diễn đầu ra đã được xét đối với bao lồi của tập hợp điểm bao gồm một hệ bất phương trình bậc nhất mô tả các mặt của bao, một đồ thị vô hướng của các mặt đó (kể cả các mặt liền kề), hoặc toàn bộ dàn mặt của bao đó.^[31] Ở hai chiều, có một cách đơn giản hơn là liệt kê các điểm là đỉnh trong cấp cyclic của chúng quanh bao này.^[2]

Với bao lồi hai chiều hoặc ba chiều, độ phức tạp tính toán của các thuật toán tương ứng thường được đo theo số điểm đầu vào ${\displaystyle n}$ và số điểm trong bao lồi ${\displaystyle h}$, có thể nhỏ hơn đáng kể so với ${\displaystyle n}$. Đối với bao trong không gian nhiều chiều thì số mặt của các chiều khác cũng có thể được quan tâm khi phân tích thuật toán. Quét Graham có thể tính bao lồi của ${\displaystyle n}$ điểm trong mặt phẳng trong thời gian ${\displaystyle O(n\log n)}$. Với các điểm ở hai và ba chiều, có một số thuật toán nhạy cảm đầu ra phức tạp hơn có thể tính được bao lồi trong thời gian ${\displaystyle O(n\log h)}$, trong đó có thuật toán Chan và thuật toán Kirkpatrick–Seidel.^[32] Với số chiều ${\displaystyle d>3}$, thời gian để tính bao lồi là ${\displaystyle O(n^{\lfloor d/2\rfloor })}$, bằng với độ phức tạp đầu ra trong trường hợp tệ nhất của bài toán.^[33] Bao lồi của một đa giác đơn trong mặt phẳng có thể được dựng trong thời gian tuyến tính.^[34]

Các cấu trúc dữ liệu bao lồi động có thể được dùng để theo dõi bao lồi của một tập hợp điểm khi thêm vào hoặc xóa đi các điểm trong tập hợp,^[35] và các cấu trúc bao lồi điểm chuyển động có thể giúp theo dõi bao lồi đối với các điểm chuyển động liên tục.^[36] Dựng bao lồi cũng là công cụ cho một số thuật toán hình học tính toán khác, chẳng hạn như thuật toán thước cặp quay dùng để tính chiều dài và đường kính của một tập hợp điểm.^[37]

Các cấu trúc liên quan

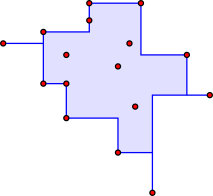
Một số hình khác có thể được xác định từ một tập hợp các điểm theo cách tương tự như với bao lồi, có thể là tập cha nhỏ nhất với tính chất nhất định, là giao của tất cả các hình chứa các điểm đó từ một họ các hình cho trước, hoặc là hợp của tất cả tổ hợp của các điểm với dạng nhất định. Ví dụ:

• Bao afin là không gian con afin nhỏ nhất của một không gian Euclid chứa một tập hợp cho trước, hoặc là hợp của tất cả tổ hợp afin của các điểm trong tập hợp đó.^[38]
• Bao tuyến tính là không gian con tuyến tính nhỏ nhất của một không gian vectơ chứa một tập hợp cho trước, hoặc là hợp của tất cả tổ hợp tuyến tính của các điểm trong tập hợp đó.^[38]
• Bao conic hoặc bao dương của một tập con của một không gian vectơ là tập hợp tất cả tổ hợp dương của các điểm trong tập con đó.^[38]
• Bao trực quan của một đối tượng ba chiều, đối với một tập hợp điểm nhìn, chứa các điểm ${\displaystyle p}$ sao cho mỗi tia từ một điểm nhìn đi qua ${\displaystyle p}$ đều cắt đối tượng đó. Một cách tương đương, nó là giao của các mặt nón (không lồi) được tạo bởi các đường biên của đối tượng đối với mỗi điểm nhìn. Trong tái cấu trúc 3D, nó là hình lớn nhất có thể có các đường biên giống nhau từ các điểm nhìn cho trước.^[39]
• Bao tròn hoặc bao alpha của một tập con của mặt phẳng là giao của tất cả các đĩa với bán kính cho trước là ${\displaystyle 1/\alpha }$ chứa tập con đó.^[40]
• Bao lồi tương đối của một tập con của một đa giác đơn hai chiều là giao của tất cả các tập cha lồi tương đối, trong đó một tập hợp nằm trong đa giác đó là tập lồi tương đối nếu nó chứa đường trắc địa giữa hai điểm bất kỳ của nó.^[41]
• Bao lồi trực giao là giao của tất cả các tập cha lồi trực giao được nối lại với nhau, trong đó một tập hợp được gọi là tập lồi trực giao nếu nó chứa tất cả các đoạn thẳng song song với trục tọa độ nối từng cặp điểm có trong nó.^[42]
• Bao lồi trực giao là một trường hợp đặc biệt của một dạng cấu trúc tổng quát hơn, bao siêu lồi, vốn có thể được xem là không gian mêtric đơn ánh nhỏ nhất chứa các điểm của một không gian mêtric cho trước.^[43]
• Bao lồi chỉnh hình là một dạng khái quát hóa của các khái niệm tương tự sang đa tạp giải tích phức, có được do nó là giao của các tập mức con của các hàm chỉnh hình chứa một tập hợp cho trước.^[44]

Tam giác đạc Delaunay của một tập hợp điểm và dạng đối ngẫu của nó, sơ đồ Voronoi, đều có liên quan đến bao lồi: tam giác đạc Delaunay của một tập hợp điểm trên ${\displaystyle \mathbb {R} ^{n}}$ có thể được xem là hình chiếu của một bao lồi trên ${\displaystyle \mathbb {R} ^{n+1}}$.^[45] Các hình alpha của một tập hợp điểm hữu hạn cho một họ gồm các đối tượng hình học (không lồi) lồng nhau mô tả hình dạng của một tập hợp điểm tại các cấp độ chi tiết khác nhau. Mỗi hình alpha đều là hợp của một số điểm trong tam giác đạc Delaunay, được chọn bằng cách so sánh bán kính đường tròn ngoại tiếp của chúng với tham số alpha. Chính tập hợp điểm đó tạo thành một điểm cuối của họ các hình đó, và bao lồi của nó tạo thành điểm cuối còn lại.^[40] Lớp lồi của một tập hợp điểm là một họ gồm đa giác lồi lồng nhau, trong đó đa giác ngoài cùng là bao lồi, với các lớp bên trong được dựng một cách đệ quy từ các điểm không phải là đỉnh của bao lồi đó.^[46]

Chỏm lồi của một đa giác là đa giác lồi lớn nhất được chứa trong nó. Nó có thể được tìm trong thời gian đa thức, nhưng số mũ của thuật toán rất cao.^[47]

Ứng dụng

Bao lồi được ứng dụng rộng rãi trong nhiều lĩnh vực. Trong toán học, bao lồi được dùng để nghiên cứu đa thức, giá trị riêng của ma trận, phần tử đơn nguyên đơn vị và một số định lý liên quan đến bao lồi trong hình học rời rạc. Trong thống kê chuẩn mạnh, bao lồi là đường viền ngoài cùng của độ sâu Tukey, là một phần quan trọng của biểu đồ túi minh họa dữ liệu hai chiều, và được dùng để xác định tập nguy cơ của các quy tắc ra quyết định ngẫu nhiên. Bao lồi của vectơ chỉ thị của nghiệm cho các bài toán tổ hợp là nội dung trọng tâm trong tối ưu hóa tổ hợp và tổ hợp đa diện. Trong kinh tế học, bao lồi có thể được dùng để áp dụng các phương pháp về tính lồi trong kinh tế cho các thị trường không lồi. Trong mô hình hóa hình học, đặc tính bao lồi đường cong Bézier hỗ trợ tìm các giao điểm của chúng, và bao lồi là một phần không thể thiếu trong việc đo thân tàu. Và trong nghiên cứu về tập tính của động vật, bao lồi xuất hiện trong một định nghĩa thường dùng về phạm vi chỗ ở.

Toán học

Đa giác Newton của đa thức đơn biến và đa diện Newton của đa thức đa biến là bao lồi của các điểm được suy ra từ số mũ của các hạng tử trong đa thức, và có thể được dùng để phân tích tính tiệm cận của đa thức và giá trị của nghiệm của đa thức đó.^[48] Bao lồi và đa thức cũng có liên hệ với nhau trong định lý Gauss–Lucas, theo đó mọi nghiệm của đạo hàm của một đa thức đều nằm trong bao lồi của các nghiệm của đa thức đó.^[49]

Trong lý thuyết phổ, miền số của một ma trận chuẩn tắc là bao lồi của các giá trị riêng của nó.^[50] Định lý Russo–Dye mô tả bao lồi của các phần tử đơn nguyên đơn vị trong một C*-đại số.^[51] Trong hình học rời rạc, định lý Radon và định lý Tverberg có liên quan đến sự tồn tại phân hoạch của các tập hợp điểm thành các tập con với bao lồi giao nhau.^[52]

Định nghĩa tập lồi là tập hợp chứa tất cả các đoạn thẳng nối các điểm của nó và bao lồi là giao của tất cả các tập cha lồi đều áp dụng được cho không gian hyperbol và không gian Euclid. Tuy nhiên, trong không gian hyperbol, còn có thể xét đến bao lồi của tập hợp điểm lý tưởng gồm những điểm không thuộc chính không gian hyperbol mà chỉ nằm trong đường biên của một mô hình không gian đó. Đường biên của bao lồi của các điểm lý tưởng của không gian hyperbol ba chiều là tương tự với bề mặt xiên trong không gian Euclid, và các tính chất mêtric của chúng đóng vai trò quan trọng trong giả thuyết hình học hóa trong tôpô ít chiều.^[53] Bao lồi hyperbol cũng được dùng khi tính tam giác đạc chính tắc của đa tạp hyperbol, hay xác định xem hai nút thắt có bằng nhau hay không.^[54]

Xem thêm mục chuyển động Brown về ứng dụng của bao lồi trong chuyển động Brown, và mục đường cong không gian về ứng dụng của bao lồi trong lý thuyết về bề mặt khai triển được.

Thống kê

Trong thống kê chuẩn mạnh, bao lồi là một trong những thành phần chủ chốt của một biểu đồ túi (bagplot), một phương pháp để minh họa phân bố của các điểm mẫu hai chiều. Các hình bao của độ sâu Tukey tạo thành một họ tập lồi lồng nhau với bao lồi nằm ngoài cùng, và biểu đồ túi cũng hiển thị một đa giác khác có hình bao với độ sâu 50% từ họ lồng nhau đó.^[55]

Trong lý thuyết quyết định thống kê, tập nguy cơ của một quy tắc ra quyết định ngẫu nhiên là bao lồi của các điểm nguy cơ của các quy tắc ra quyết định tất định nằm dưới nó.^[56]

Tối ưu hóa tổ hợp

Đối tượng nghiên cứu trọng tâm trong tối ưu hóa tổ hợp và tổ hợp đa diện là bao lồi của vectơ chỉ thị của nghiệm cho một bài toán tổ hợp. Nếu mặt của các đa diện đó có thể tìm được, mô tả đa diện là giao của các nửa không gian, thì các thuật toán dựa trên quy hoạch tuyến tính có thể được dùng để tìm nghiệm tối ưu.^[57] Bao lồi của các vectơ trọng số của các nghiệm đó, một dạng khác của bao lồi, cũng được dùng trong tối ưu hóa đa mục tiêu. Ta có thể cực đại hóa bất kỳ tổ hợp tựa lồi của các trọng số bằng cách tìm và kiểm tra từng đỉnh của bao lồi, hiệu quả hơn nhiều so với khi kiểm tra tất cả các nghiệm có thể có.^[58]

Kinh tế

Trong mô hình Arrow–Debreu của cân bằng kinh tế tổng thể, đại diện kinh tế được giả thiết là có tập ngân sách lồi và ưa thích lồi. Các giả thiết này của tính lồi trong kinh tế có thể được dùng để chứng minh sự tồn tại của một cân bằng như thế. Khi dữ liệu kinh tế trong thực tế là phi lồi thì có thể chuyển dữ liệu này sang trạng thái lồi bằng cách lấy bao lồi của nó. Định lý Shapley–Folkman có thể được áp dụng để chứng minh rằng với các thị trường lớn thì phép xấp xỉ này là chính xác và dẫn đến một "tựa cân bằng" đối với thị trường phi lồi ban đầu.^[59]

Mô hình hóa hình học

Trong mô hình hóa hình học, một trong những tính chất then chốt của đường cong Bézier là nó nằm trong bao lồi của các điểm kiểm soát của nó. Cái gọi là "đặc tính bao lồi" này có thể được áp dụng để nhanh chóng tìm ra giao điểm của các đường cong như vậy chẳng hạn.^[60]

Trong thiết kế tàu thuyền, chu vi xích thân tàu (chain girth) là một độ đo kích thước của một tàu buồm, được xác định bằng bao lồi của mặt cắt ngang thân tàu. Nó khác với chu vi mặt ngoài thân tàu (skin girth) là chu vi của chính mặt cắt đó ngoại trừ đối với tàu thuyền có bao lồi.^[61]

Tập tính học

Bao lồi thường được xem là đa giác lồi nhỏ nhất trong tập tính học, một lĩnh vực nghiên cứu hành vi của động vật, ở đó nó là cách tiếp cận cổ điển để ước lượng phạm vi chỗ ở của một loài động vật dựa vào các điểm mà loài động vật đó được quan trắc.^[62] Các điểm ngoại lai có thể làm kích thước của đa giác đó tăng một cách quá mức; một hướng tiếp cận khác để hạn chế tình trạng này là chỉ ước lượng dựa trên tập con của các điểm quan trắc, chẳng hạn như chọn một trong các lớp lồi sát với một tỉ lệ mật độ điểm dữ liệu làm mẫu,^[63] hoặc áp dụng phương pháp bao lồi địa phương bằng cách hợp bao lồi của láng giềng của các điểm.^[64]

Vật lý lượng tử

Trong vật lý lượng tử, không gian trạng thái của một hệ thống lượng tử — tập hợp tất cả các cách hệ thống có thể được thiết lập — là một bao lồi có điểm cực biên là các toán tử nửa xác định dương gọi là trạng thái thuần và các điểm ở phía trong gọi là trạng thái hỗn hợp.^[65] Định lý Schrödinger–HJW chứng minh rằng một trạng thái hỗn hợp bất kỳ có thể được viết thành tổ hợp lồi của các trạng thái thuần theo nhiều cách khác nhau.^[66]

Nhiệt động lực học

Một bao lồi trong nhiệt động lực học đã được Josiah Willard Gibbs xác định trong bài báo năm 1873,^[68] dù nó được xuất bản từ trước khi thuật ngữ "bao lồi" có tên gọi như hiện tại. Trong một tập hợp các mức năng lượng của các hệ số tỷ lượng đối với một vật liệu, chỉ có mức năng lượng với những giá trị đo nằm ở bao lồi dưới mới bền vững. Khi loại đi một điểm thì khoảng cách của nó tới bao này chỉ độ bền của trạng thái đó.^[69]

Lịch sử

Bao lồi của các điểm trong mặt phẳng xuất hiện lần đầu tiên dưới dạng đa giác Newton trong thư của Isaac Newton gửi Henry Oldenburg vào năm 1676.^[70] Thuật ngữ convex hull trong tiếng Anh xuất hiện sớm nhất từ công trình của Garrett Birkhoff (1935), và cụm từ tương ứng trong tiếng Đức xuất hiện sớm hơn, chẳng hạn như trong bình duyệt về Kőnig (1922) của Hans Rademacher. Một số thuật ngữ khác như convex envelope cũng được sử dụng trong khoảng thời gian này.^[71] Đến năm 1938, theo Lloyd Dines, từ convex hull đã trở thành tiêu chuẩn, và Dines thêm rằng ông thấy đó là điều đáng tiếc, vì nghĩa thông tục của từ hull có thể được hiểu rằng nó chỉ bề mặt của một hình, trong khi bao lồi thực tế còn chứa thêm cả phần bên trong chứ không chỉ có phần bề mặt đó.^[72]

Chú thích

Tham khảo

Đọc thêm

• Đỗ Văn Lưu; Phan Huy Khải (2000), “Chương I: Tập lồi”, Giải tích lồi, Hà Nội: Nhà xuất bản Khoa học và Kỹ thuật, tr. 3–37. Đặc biệt xem mục "1.1.2 Bao lồi và bao lồi đóng", tr. 6–9.

Liên kết ngoài

• Hazewinkel, Michiel biên tập (2001), “Convex hull”, Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4
• Weisstein, Eric W., "Convex Hull" từ MathWorld.