Poisson dağılımı

Poisson

Olasılık kütle fonksiyonu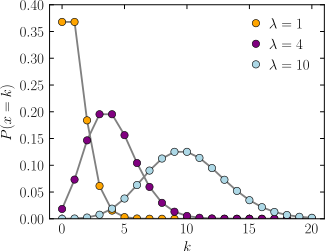 Yatay eksen indeks k . Fonksiyon yalnızca k'nın tam sayı değerleri için geçerlidir. Noktaları bağlayan çizgiler süreklilik göstermez; kullanıcıya yardımcı olmak üzere çizilmişlerdir.
Yığmalı dağılım fonksiyonu Yatay eksen indeks k .
Parametreler	${\displaystyle \lambda \in (0,\infty )}$
Destek	${\displaystyle k\in \{0,1,2,\ldots \}}$
Olasılık kütle fonksiyonu (OYF)	${\displaystyle {\frac {e^{-\lambda }\lambda ^{k}}{k!}}\!}$
Birikimli dağılım fonksiyonu (YDF)	${\displaystyle {\frac {\Gamma (\lfloor k+1\rfloor ,\lambda )}{\lfloor k\rfloor !}}\!{\text{ eğer }}k\geq 0}$ (burada ${\displaystyle \Gamma (x,y)}$ Tamamlanmamış gama fonksiyonudur)
Ortalama	${\displaystyle \lambda \,}$
Medyan	yaklaşık olarak ${\displaystyle \scriptstyle \lfloor \lambda +1/3-0.02/\lambda \rfloor }$
Mod	${\displaystyle \scriptstyle \lfloor \lambda \rfloor }$ ve ${\displaystyle \lambda -1}$ eğer ${\displaystyle \lambda }$ bir tam sayı ise
Varyans	${\displaystyle \lambda \,}$
Çarpıklık	${\displaystyle \lambda ^{-1/2}\,}$
Fazladan basıklık	${\displaystyle \lambda ^{-1}\,}$
Entropi	${\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\ln(k!)}{k!}}}$ (büyük ${\displaystyle \lambda }$ değeri için) ${\displaystyle {\frac {1}{2}}\log(2\pi e\lambda )-{\frac {1}{12\lambda }}-{\frac {1}{24\lambda ^{2}}}}$${\displaystyle -{\frac {19}{360\lambda ^{3}}}+O\left({\frac {1}{\lambda ^{4}}}\right)}$
Moment üreten fonksiyon (mf)	${\displaystyle \exp(\lambda (e^{t}-1))\,}$
Karakteristik fonksiyon	${\displaystyle \exp(\lambda (e^{it}-1))\,}$

Poisson dağılımı, (okunuşu: puason dağılımı) olasılık kuramı ve istatistik bilim kollarında bir ayrık olasılık dağılımı olup belli bir sabit zaman birim aralığında meydana gelme sayısının olasılığını ifade eder. Bu zaman aralığında ortalama olay meydana gelme sayısının bilindiği ve herhangi bir olayla onu hemen takip eden olay arasındaki zaman farkının, önceki zaman farklarından bağımsız oluştuğu kabul edilir.

Poisson dağılımı çok kere belirli sabit zaman aralığı birimleri bulunan problemlere uygulanmakla beraber, diğer birimsel aralıklı problemlere de (yani birim uzaklık, alan veya hacim içeren problemlere de) başarı ile uygulanabilir.

Örnekler

Poisson dağılımı Poisson süreci ile birlikte ortaya çıkar. Poisson süreci aralıklı karakterde olan (yani 0, 1, 2, 3 .. kere meydana çıkan) bazı olgularin bir birim zaman, alan, mekân veya hacimde sabit bir olasılıkla oluşması şeklini alır. Bu çeşit olaylara ve Poisson dağılımının uygulanmasına örnekler şunlardır:

• Prusya süvari birliklerinde her bir yıl at ve katır tepmeleri ile ölen asker sayısı: Bu klasik örnek 1868'de Ladislaus Josephovich Bortkiewicz tarafından bir kitapta yayınlanmış ve çok tanınmış bir örnek olarak yıllarca askeri ve sivil yüksek okul öğrencilerine verilmiştir.
• Bir saat aralığında belli bir Internet sitesine gelen bağlantılar sayısı;
• Yarım saat içinde bir nakliyat deposuna yükleme-boşatılma için gelen kamyon sayısı;
• Her bir beş dakika içinde bir telefon cevap merkezine gelen telefonlar sayısı;
• Belli bir trafik kavşağından 1 dakika içinde geçen otomobil sayısı;
• Belli bir zaman aralığında bir büyük binada yanıp çalışması duran floresan lambalarının sayısı;
• Bir mucit kişinin çalışma hayatı boyunca patentini aldığı keşifler sayısı;

[Not: Birbirini takip eden Poisson tipi olaylar arasındaki aralık karşılıklı ilişkili olarak bir üstel dağılım olur. Örneğin, bir floresan ampülünun çalışma süresi veya otobüslerin gelmesi arasındaki bekleme zamanı.]

Tarihçe

Bu dağılım ilk defa Siméon-Denis Poisson (1781–1840) tarafından diğer olasılık hakkındaki yazıları ile birlikte 1838'de yayınlanan Recherches sur la probabilité des jugements en matières criminelles et matière civile ("Ceza hukuku ve medeni hukuk alanlarındaki hükümlerin olasılığı üzerinde araştırmalar") adındaki eserinde ortaya atılmıştır.

Nadir olaylar için Poisson dağılımı

Poisson dağılımının genel odaklandığı rassal değişken bir sayılabilen olaydır; bu olay belli bir sabit uzunlukta olan (genellikle zaman) aralıkta ayrık olarak ortaya çıkar ve bu aralıkta gözlenen olayların sayısı Poisson dağılım için rassal değişkendir. Bu sabit aralıkta ortaya çıkan olaylar sayısının beklenen değeri (ortaya çıkmanın ortalama sayısı) λ olarak sabittir ve bu ortalama değer aralık uzunluğuna orantılıdır. Eğer her 4 dakikalık zaman aralığı içinde ortalama 5 olay meydana geliyorsa, sabit 8 dakikalık aralıkta ortalama 10 (=8x5/4) olay ortaya çıkar. Herhangi bir negatif olmayan bir tam sayı olan k sayıda (k = 0, 1, 2, 3...) olay ortaya çıkma olasılığı şöyle ifade edilir:

${\displaystyle f(k,\lambda )={\frac {\lambda ^{k}e^{-\lambda }}{k!}},\,\!}$

burada

• e, doğal logaritmanın tabanı (e = 2.71828...);
• k, olasılığı fonksiyon ile verilmekte olan olayın ortaya çıkma sayısı;
• k!, k için faktöriyel
• λ verilen sabit aralıkta ortaya çıkma sayısının beklenen değeri; bir pozitif gerçel sayı.

Bu k'nin fonksiyonu Poisson dağılım için olasılık kütle fonksiyonu olur.

Poisson dağılımı için λ parametresi yalnızca beklenen değer, yani ortaya çıkan ${\displaystyle \scriptstyle \langle k\rangle }$ sayıda olay için bir ortalama, değildir. Aynı zamanda

${\displaystyle \scriptstyle \sigma _{k}^{2}\ {\stackrel {\mathrm {def} }{=}}\ \langle k^{2}\rangle -\langle k\rangle ^{2}}$

yani varyans da olur. Böylece gözlenen olay meydan çıkış sayısı bir ortalama değer λ ile bir standart sapması ${\displaystyle \scriptstyle \sigma _{k}\,=\,{\sqrt {\lambda }}}$ olması niteliklerini taşıyan bir olasılık dağılımı, Poisson dağılımı, göstermektedir.

Genellikle bir Poisson dağılımı büyük sayıda olay ortaya çıkabilmesi mümkün olduğu, ama bu ortaya çıkması mümkün olayların nadir olduğu kabul edilen, sistemlerde uygulanabilir. Bilimsel alanlarda klasik örnekler atomların nükleer parçalanması; verilen bir DNA zincirinde ortaya çıkan mutasyon sayısı vb. Bu örneklerle ve diğer birçok örneğin için, ortaya çıkan nadir olay sayısı ayrık denemelerin sonucudur ve daha kesinlikle bir binom dağılım kullanılarak model haline getirilebilirler. Fakat n ve λ/n parametreli bir binom dağılımı (yani her deneme için λ/n başarı olasılığı olan n sayıda deneme için belirli bir başarı sayısı için olasılık dağılımı), deneme sayısı n büyüyüp limitte sonsuzluğa yaklaştıkça, beklenen değeri λ olan bir Poisson dağılıma yakınsallaşır. Bu limit bazen nadir olaylar kuralı olarak anılmaktadır. Bu ifade bir bakıma yanıltıcıdır; çünkü birçok Poisson dağılımı ile modellenebilen olaylar arasında birçoğu (örneğin bir otobüs durağına yarım saat aralığında gelen otobüs sayısı; bir mobil telefona bir saat aralığında gelen çağrı sayısı gibi) hiç de nadir olmayan olaylar bulunur. Ancak binom dağılımının büyük sayılar için hesaplanması faktöriyel sayılar kullanılması gerektirdiği için, bu uzun hesaplama biraz sıkıcı görülebilmekte ve bu nedenle Poisson dağılımı yaklaşık olarak binom dağılım yerine kullanılmaktadır.

Binom dağılımından limitte Poisson dağılım olasılık kütle fonksiyonunun çıkartılmasının matematiksel kanıtı şöyle yapılır:

Önce, değişkenler hesabı (calculus) içinde kullanılan limitin şöyle ifade edildiği hatırlanır:

${\displaystyle \lim _{n\to \infty }\left(1-{\lambda \over n}\right)^{n}=e^{-\lambda }.}$

p = λ/n eşitliği bu ifade içine konulursa, şu genel denkleme varılır:

${\displaystyle \lim _{n\to \infty }\Pr(X=k)=\lim _{n\to \infty }{n \choose k}p^{k}(1-p)^{n-k}=\lim _{n\to \infty }{n! \over (n-k)!k!}\left({\lambda \over n}\right)^{k}\left(1-{\lambda \over n}\right)^{n-k}}$

Şimdi bu son ifade biraz daha açılır ve şu elde edilir:

${\displaystyle =\lim _{n\to \infty }\underbrace {\left({n \over n}\right)\left({n-1 \over n}\right)\left({n-2 \over n}\right)\cdots \left({n-k+1 \over n}\right)} \ \underbrace {\left({\lambda ^{k} \over k!}\right)} \ \underbrace {\left(1-{\lambda \over n}\right)^{n}} \ \underbrace {\left(1-{\lambda \over n}\right)^{-k}} }$

Limitte, ilk parantez içindeki ifade 1 e yakınsama gösterir (yani n ∞'a yaklaştıkça, ilk parantezdeki ifade 1'e yakınsar) ve ikinci parantez içindeki ifade, ifade içinde n olmaması nedeniyle, sabit kalır; üçüncü parantez içindeki ifade e^−λ değerine yakınsar ve son olarak da dördüncü parantezdeki ifade, 1 e yakınsar. Sonuçta, limitte şu ortaya çıkar:

${\displaystyle {\lambda ^{k}e^{-\lambda } \over k!}.\,\!}$

Daha genel olarak, n ve p_n parametreleri olan binom rassal değişkenler için bir sıra Binom ifadesi

${\displaystyle \lim _{n\rightarrow \infty }np_{n}=\lambda ,}$

olursa, bu seri dağılımda ortalaması λ olan bir Poisson rassal değişkeni için serilere yakınlaşır.^[1]

Örnek:

${\displaystyle {\displaystyle k}}$	${\displaystyle P(k{\text{ taşkın seli 100 yılda}})}$
0	0.368
1	0.368
2	0.184
3	0.061
4	0.015
5	0.003
6	0.0005

Bir nehirde ortalama olarak her 100 yılda bir taşkın seli meydana gelir. Poisson modelinin uygun olduğunu varsayarak, 100 yıllık bir aralıkta k = 0, 1, 2, 3, 4, 5 veya 6 taşkın seli olma olasılığını hesaplayın.

Ortalama olay oranı 100 yılda bir taşma olduğundan, λ = 1

${\displaystyle P(k{\text{ taşkın seli 100 yıl içinde}})={\frac {\lambda ^{k}e^{\lambda }}{k!}}={\frac {1^{k}e^{-1}}{k!}}}$

${\displaystyle P(k={\text{0 taşkın seli 100 yıl içinde}})={\frac {1^{0}e^{-1}}{0!}}={\frac {e^{-1}}{1}}\approx 0.368}$

${\displaystyle P(k={\text{1 taşkın seli 100 yıl içinde}})={\frac {1^{1}e^{-1}}{1!}}={\frac {e^{-1}}{1}}\approx 0.368}$

${\displaystyle P(k={\text{2 taşkın seli 100 yıl içinde}})={\frac {1^{2}e^{-1}}{2!}}={\frac {e^{-1}}{2}}\approx 0.184}$

Özellikler

• Poisson dağılımı gösteren rassal bir değişken için beklenen değer ve varyans değeri de λdır. Poisson dağılımının yüksek momentleri λ terimleri ile oluşan (matematiksel kombinatorik kuramında anlamlı olan katsayıları bulunan) Touchard polinomlarıdır. Eğer Poisson dağılımı için beklenen değer 1 ise, o zaman Dobinski'nin formülüne göre ninci moment n büyüklüğünde olan set bölünümlerinin sayısına eşittir.
• Tam sayılı olmayan bir λ lambda parametreli Poisson dağılımı gösteren bir rassal değişkenin mod değeri, λ 'dan küçük olan en büyük pozitif tam sayıya, yani ${\displaystyle \scriptstyle \lfloor \lambda \rfloor }$ 'ya, eşittir.
• Poisson dağılımı gösteren rassal değişkenlerin toplamı:

Eğer ${\displaystyle X_{i}\sim \mathrm {Poi} (\lambda _{i})\,}$ ifadesi ${\displaystyle \lambda _{i}}$ parametresi ile Poisson dağılımı gösteriyor ve ${\displaystyle X_{i}}$ terimleri bağımsız iseler, o halde

${\displaystyle Y=\sum _{i=1}^{N}X_{i}\sim \mathrm {Poi} \left(\sum _{i=1}^{N}\lambda _{i}\right)\,}$

ifadesi de parametresi toplama katılan parametre toplamlarından olan bir Poisson dağılımı gösterir.

• Beklenen değeri λ olan Poisson dağılımınin moment üreten fonksiyonu şu ifade ile verilir:

${\displaystyle \mathrm {E} \left(e^{tX}\right)=\sum _{k=0}^{\infty }e^{tk}f(k;\lambda )=\sum _{k=0}^{\infty }e^{tk}{\lambda ^{k}e^{-\lambda } \over k!}=e^{\lambda (e^{t}-1)}.}$

• Poisson dağılımı için tüm kümülantlar beklenen değer olan λya eşittirler. Poisson dağılımı için ninci faktöriyel moment λⁿ olur
• Poisson dağılımları sonsuz olarak bölünebilir olasılık dağılımlarıdır.
• Poi(λ₀) ile Poi(λ) arasındaki yönlendirilmiş Kullback-Leibler ayrılımı şöyle ifade edilir;

${\displaystyle \Delta (\lambda ||\lambda _{0})=\lambda \left(1-{\frac {\lambda _{0}}{\lambda }}+{\frac {\lambda _{0}}{\lambda }}\log {\frac {\lambda _{0}}{\lambda }}\right).}$

Poisson dağılımı ile üretilen rassal değişkenlerin simülasyonu

Poisson dağılımlı rassal sayıları üretmek için en basit yollardan birisi Knuth tarafından aşağıdaki gibi bir bilgisayar algoritmasıyla verilmiştir:^[2]

algoritma poisson rassal sayı üretimi (Knuth):
    init:
        Let L ← e−λ, k ← 0 and p ← 1.
    do:
         k ← k + 1.
         [0,1] aralığı içinde birörnek dağılımlı rassal sayı u üret ve let p ← p × u.
    while p ≥ L.
    return k − 1.

Basit olmakla beraber, karmaşıklık λ ile doğrusal olarak oranlıdır. Bu sorun etkisini azaltmak için çeşitli diğer algoritmalar geliştirilmiştir.^[3][4]

İlişkili dağılımlar

• Eğer ${\displaystyle X_{1}\sim \mathrm {Pois} (\lambda _{1})\,}$ ve ${\displaystyle X_{2}\sim \mathrm {Pois} (\lambda _{2})\,}$ ise, o halde ${\displaystyle Y=X_{1}-X_{2}}$ farkı bir Skellam dağılımı gösterir.
• Eğer ${\displaystyle X_{1}\sim \mathrm {Pois} (\lambda _{1})\,}$ ve ${\displaystyle X_{2}\sim \mathrm {Pois} (\lambda _{2})\,}$ bağımsızlarsa ve ${\displaystyle Y=X_{1}+X_{2}}$ ise, o zaman ${\displaystyle Y=y}$ya koşullu ${\displaystyle X_{1}}$ dağılımı, bir binom dağılımı olur. Özellikle, ${\displaystyle X_{1}|(Y=y)\sim \mathrm {Binom} (y,\lambda _{1}/(\lambda _{1}+\lambda _{2}))\,}$ olur. Daha genel olarak, eğer X₁, X₂,...,X_n rassal değişkenleri, parametreleri
  λ₁, λ₂,..., λ_n olan Poisson dağılımı gösteriyorlarsa, o zaman ${\displaystyle X_{i}\left|\sum _{j=1}^{n}X_{j}\right.\sim \mathrm {Binom} \left(\sum _{j=1}^{n}X_{j},{\frac {\lambda _{i}}{\sum _{j=1}^{n}\lambda _{j}}}\right)}$.
• Eğer denemeler sayısı limitte sonsuza doğru yaklaşır ve başarı sayısının beklenen değeri sabit kalırsa, bu binom dağılım limitte Poisson dağılıma yaklaşacağı ispat edilmiştir. Bu nedenle Poisson dağılım, eğer n yeterce büyük ve p yeterce küçük ise, bir binom dağılım yerine yaklaşım olarak kullanılabilir. Alışılagelen bir kurala göre, eğer n en aşağı 20 ise ve p 0,05'e eşit veya daha küçük ise, Poisson dağılımı binom dağılımının iyi bir yaklaşımı olacaktır. Bu kurala göre eğer n ≥ 100 ve np ≤ 10 ise, bu yaklaşım mükemmel olur.^[5]
• Yeter derecede yüksek λ değeri (diyelim λ>1000) için, ortalaması λ ve varyansı λ olan bir normal dağılım, Poisson dağılım için çok iyi bir yaklaşım olur. Eğer λ 10'dan biraz büyük ise, bu halde normal dağılım ancak uygun bir süreklilik doğrulaması kullanılırsa uygun bir yaklaşım olabilir. Başka bir deyim ile, eğer P(X ≤ x) ifadeleri P(X ≤ x + 0.5) ile değiştirilirse

${\displaystyle F_{\mathrm {Poisson} }(x;\lambda )\approx F_{\mathrm {normal} }(x;\mu =\lambda ,\sigma ^{2}=\lambda )\,}$ olur.

• Eğer bir sabit zaman aralığı içinde bir hizmet alanına gelenler sayısı, ortalaması ${\displaystyle \lambda }$ olan bir Poisson dağılımına uygun ise, o halde gelişler-arası zaman aralıkları, oran parametresi ${\displaystyle 1/\lambda }$ olan, bir üstel dağılım gösterir.

Parametre tahmini

Maksimum olabilirlik

k_i için n tane ölçülmüş değer kapsayan bir örneklem alınsın. Bu örneklemin kökenindeki Poisson dağılım gösteren anakütle için Poisson parametresi olan λ için bir uygun bir kestirim değeri bulunması hesaplama hedefidir.

Bu kestirimi maksimum değişebilirlik yöntemi ile bulmak için önce bir log-değişebilirlilik fonksiyonu şöyle biçimlendirilir:

${\displaystyle L(\lambda )=\ln \prod _{i=1}^{n}f(k_{i}\mid \lambda )\!}$

${\displaystyle =\sum _{i=1}^{n}\ln \!\left({\frac {e^{-\lambda }\lambda ^{k_{i}}}{k_{i}!}}\right)\!}$

${\displaystyle =-n\lambda +\left(\sum _{i=1}^{n}k_{i}\right)\ln(\lambda )-\sum _{i=1}^{n}\ln(k_{i}!).\!}$

λ ile L fonksiyonunun türevi alınıp bu türev sıfıra eşitlenirse

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} \lambda }}L(\lambda )=0\iff -n+\left(\sum _{i=1}^{n}k_{i}\right){\frac {1}{\lambda }}=0\!}$

ifadesi ortaya çıkar. λ için çözüm yapılırsa λ için maksimum olabilirlilik kestirimini(MOK) şöyle buluruz:

${\displaystyle {\widehat {\lambda }}_{\mathrm {MOK} }={\frac {1}{n}}\sum _{i=1}^{n}k_{i}.\!}$

Her gözlem için ortalama λ olduğu için bu ifadenin beklenen değeri de λ olur. Bu nedenle bu kestirim λ için bir yansiz kestirim olur. Bunun kestirim varyans değeri Cramer-Rao alt sınırına ulaşıp geçtigi için, bu kestirim bir etkin kestirim de olur.

Bayes tipi çıkarımsal analiz

Bayes tipi çıkarımsal analiz için Poisson dağılımının oran parametresi olan λ için eşlenik öncel bir gamma dağılımı gösterir. Şu ifadeye göre

${\displaystyle \lambda \sim \mathrm {Gamma} (\alpha ,\beta )\!}$

λnin bir Gamma olasılık yoğunluk fonksiyonuna göre dağılım gösterdiğini; gnin bir şekil parametresi olan α ile bir ters ölçek parametresi olan β ile parametrelenmiş olduğunu, şöyle gösterilsin:

${\displaystyle g(\lambda \mid \alpha ,\beta )={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\;\lambda ^{\alpha -1}\;e^{-\beta \,\lambda }\qquad {\mbox{for}}\ \lambda >0\,\!.}$

O zaman, daha önce olduğu gibi n sayıda ölçülmüş değerden oluşan örneklem k_i ve bir Gamma(α, β) dağılımlı önsel verilmiş ise, sonsal dağılım şu olur:

${\displaystyle \lambda \sim \mathrm {Gamma} \left(\alpha +\sum _{i=1}^{n}k_{i},{\frac {1}{{\frac {1}{\beta }}+n}}\right).\!}$

Sonsal ortalama olan E[λ] limitte ${\displaystyle \alpha \to 0,\ \beta \to 0}$ doğru gittikçe maksimum olabilirlik kestirimi olan ${\displaystyle {\widehat {\lambda }}_{\mathrm {MLE} }}$ ifadesine yaklaşır.

Eklecek verilerin sonsal kestirimci dağılımı bir Gamma-Poisson dağılım yani bir negatif binom dağılımı olur.

Küçük sayılar kuralı

Kural sözcüğü istatistik bilimi içinde olasılık dağılımı kavramı ile eş anlamlı olarak kullanılmaktadır. Kurala göre yakınsama kavramı dağılımda yakınsama ile aynı anlamda kullanılmaktadır. Buna dayanarak Poisson dağılımı bazen küçük sayılar kuralı olarak anılmaktadır. Buna neden bu dağılımın, nadir olacağı kabul edilmekle beraber, birçok fırsatta ortaya çıkabilen bir olayın ortaya çıkma sayısını açıklayan olasılık dağılımı olmasıdır. 1898'de Ladislaus Bortkiewicz'in Poisson dağılımı hakkında yayınladığı kitabın adı Küçük Sayılar Kuralıdır. Bazı matematik tarihçileri buna ithafen Poisson dağılımının adının da Bortkiewicz dağılımı olmasını istemişlerdir.[2]

Ayrıca bakınız

• Bileşik Poisson dağılımı
• Tweedie dağılımı
• Poisson süreci
• Poisson regresyonu
• Poisson dağılımı tablosu
• Kuyruk kuramı
• Erlang dağılımı n sayıda olayın tümüyle ortaya çıkmasına kadar bekleme zamanlarını tanımlar. Zaman içinde dağılım gösteren olaylar için Poisson dağılımı, daha önceden aralığı sabit olarak tayin edilmiş zaman birimi içinde ortaya çıkan olay sayısını verir; Erlang dağılımı ise ninci olayın olup bitmesine kadar geçen zamanının olasılık dağılımını inceler.
• Skellam dağılımı: Mutlaka aynı asıl dağılımdan ortaya çıkmayan iki Poisson değişirin farkının dağılımını verir.
• Tamamlanmamış gamma fonksiyonu: Yığmalı olasılık fonksiyonunun hesaplanması için kullanılır.
• Dobinski'nin formülü: Poisson dağılımı için momentlerin kombinatrik hesapla yorumlanması.
• Schwarz formülü
• Robbins ön kuramı: Empirik Bayes yönteminin Poisson dağılıma bağlı olduğunu gösteren bir ön kuram.

Kaynakça

Dış bağlantılar

Online görselleştirme aletleri

• SOCR distribution GUI22 Şubat 2008 tarihinde Wayback Machine sitesinde arşivlendi.
• TAMU's Interactive Poisson Distribution3 Şubat 2008 tarihinde Wayback Machine sitesinde arşivlendi.

İnternet siteleri

• Poisson Dağılımı Hesaplama
• Kuyruk kuramı için temel bilgiler
• M/M/1 tipi kuyruk sistemi7 Şubat 2008 tarihinde Wayback Machine sitesinde arşivlendi.
• Mühendislik İstatistiği Elkitabı: Poisson dağılımı15 Şubat 2008 tarihinde Wayback Machine sitesinde arşivlendi.
• QWiki'de Poisson dağılımı
• Poisson Türetilmesi 1: Bir Binom dağılımı için sürekli limit
• Poisson Türetilmesi 2: Üretici fonksiyon yaklaşımı
• Poisson Türetilemsi 3: Bekleme-zamanı dağılımının toplamı
• PoissoNed! Spor için olasılık hesaplayıcısı14 Şubat 2008 tarihinde Wayback Machine sitesinde arşivlendi.
• xkcd21 Şubat 2008 tarihinde Wayback Machine sitesinde arşivlendi. Poisson dağılımı kapsayan bir web-komik.