Birim çember

Birim çember Matematikte, yarıçapı bir birim olan çembere birim çember denir. Çoğunlukla, özellikle trigonometride, Öklid düzlemine göre Kartezyen koordinat sisteminde, merkezi orijin üzerinde (0,0) olan ve yarıçapı bir birim olan çemberdir. n birim çember sıklıkla S¹; olarak ifade edilir. Genellikle daha büyük boyutları ise birim küredir. (x,y) birim çember üzerinde bir nokta olduğunda, |x| ve |y|, dik olan ve hipotenüsü bir olan üçgenin diğer kenar uzunluklarıdır. Bu nedenle, Pisagor teoremine göre, x ve y bu denklemi karşılamaktadır.

${\displaystyle x^{2}+y^{2}=1.}$

Bir birim çember örneklemesidir. t değeri ölçülen açının değerine eşittir.

Bütün x değerleri için x² = (−x)² olduğu için, birim çember üzerinde x ve y eksenlerinin herhangi bir noktası yine birim çember üzerindedir. Yalnızca birinci bölgedeki değil, birim çember üzerinde alınan bütün noktalar(x,y) bu denklemi sağlamaktadır. Ayrıca, diğer diğer birim çemberleri tanımlamak için farklı uzaklık kavramları da kullanılabilir; Rieman çemberi gibi. Fazladan örnekler için matematik standartlarındaki başlıklara bakabilirsiniz.

Karmaşık düzlemlerde

Birim çember, karmaşık sayıların temeli olarak düşünülebilir.

${\displaystyle z=\,\mathrm {e} ^{it}\,=\cos(t)+i\sin(t)\,}$

Bu formül Euler eşitliğidir.

Birim çemberde trigonometrik fonksiyonlar

Bir trigonometrik fonksiyon olan kosinüs and sinüs birim çember üzerinde tanımlanabilir. (x,y) birim çember üzerinde bir nokta olsun, orijin(0,0) ve (x,y) arasında oluşturulan çizgi pozitif x ekseninden bir t açısı oluşturur(saat yönünün tersinde döndüğünde pozitif yöndedir).

${\displaystyle \cos(t)=x\,\!}$

${\displaystyle \sin(t)=y.\,\!}$

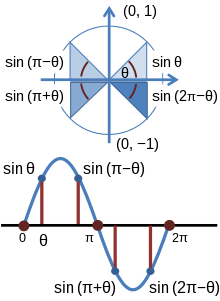
Bu denklem x² + y² = 1 şu bağıntıyı verir:

${\displaystyle \cos ^{2}(t)+\sin ^{2}(t)=1.\,\!}$

Birim çember ayrıca sinüs ve kosinüs fonksiyonlarının periyodik fonksiyon olduklarını da gösterir,

${\displaystyle \cos t=\cos(2\pi k+t)\,\!}$

${\displaystyle \sin t=\sin(2\pi k+t)\,\!}$

Herhangi bir k tam sayısı için. Birim çember üzerinde kurulan üçgenler de trigonometrik fonksiyonların periyodikliğini göstermek için kullanılabilir. Birim çember üzerinde seçilen bir P(x,y) noktası originle QA yarıçapını oluşturmaktadır ve pozitif x ekseni kolunda bir t açısına 0 < t < π/2 sahiptir. Şimdi bir Q(x₁,0) noktası düşünün, kesişimleri PQ ${\displaystyle \perp }$ OQ. Sonuç, bir dik üçgendir ΔOPQ ile ∠QOP = t. Çünkü, PQ y₁ uzunluğuna, OQ x₁ uzunluğuna ve QA’nın uzunluğu 1’dir, sin(t) = y₁ and cos(t) = x₁. Bu eşdeğerliğini kuran, OR yarıçaplı aynı açılı çember üzerinde bir nokta olan R(−x₁,y₁) x ekseninin negatif kolundadır. Şimdi bir nokta düşünün S (−x₁,0) ve kesişimleri RS ${\displaystyle \perp }$ OS. Sonuç bir dik üçgendir ΔORS ile ∠SOR = t. Bu, bu nedenle görülebilir, çünkü ∠ROQ = π−t, R (cos(π−t)noktası, sin(π−t)) aynı yöntemle P (cos(t),sin(t))noktasıdır. Bunun sonucu olarak, (−x₁,y₁) ifadesi (cos(π−t),sin(π−t)) ifadesine ve (x₁,y₁) ifadesi de (cos(t),sin(t)) bu ifadeye denktir. Bu doğru sin(t) = sin(π−t) ve −cos(t) = cos(π−t). Bu benzer bir tarzla anlamlandırılabilir tan(π−t) = −tan(t) bu yüzden, tan(t) = y₁/x₁ and tan(π−t) = y₁/(−x₁). Yukarıdaki basit gösterim bir denklemde görülebilir sin(π/4) = sin(3π/4) = 1/sqrt(2). Dik bir üçgen, sinüs, kosinüs ve diğer trigonometrik fonksiyonlarla çalışıldığında yalnızca 0’dan büyük π/2’den küçük olan açılar anlamlandırılabilir. Ancak, birim çember ile tanımlanmış bu işlevler için ölçülen açısı 2π'den büyük olanlarda bile bu gerçek değerleri elde etmek mümkündür. Aslında, altı standart trigonometrik fonksiyonlar; sinüs, kosinüs, tanjant, kotanjant, sekant, kosecant gibi arkaik fonksiyonları versine ve exsecant, sağda gösterildiği gibi bir birim çemberin açısından geometrik olarak tanımlanabilir. Birim çember kullanarak,birçok açı için herhangi bir trigonometrik fonksiyon değeri, toplam ve fark formüllerini kullanarak bir hesap makinesi kullanmadan hesaplanabilir.

Çember grubu

Kompleks sayılar Öklid düzlemi üzerindeki noktalar ile tespit edilebilir.Yani, a + bi sayısı (a, b) noktası olarak tanımlanabilir. Bu tanımlama altında, birim çember, çember grubu diye bilinen çarpmanın altında bir gruptur. Düzlemde çarpma ${\displaystyle \cos \theta +i\sin \theta }$ &theta açısıyla saat yönünün tersinde bir dönme oluşturur. Bu grup matematikte ve bilimde önemli uygulamalara sahiptir.

Karmaşık düzlemlerde

Julia seti ve ayrık olmayan dinamik sistemi ile evrim fonksiyonu :

${\displaystyle f_{0}(x)=x^{2}\,}$

Bu bir birim çemberdir. Bu, yaygın olarak dinamik sistemlerin çalışmasında kullanılan çok basit bir durumdur.

Dış bağlantılar

Vikikitapta bu konu hakkında daha fazla bilgi var:

Trigonometry/The unit circle

• Eric W. Weisstein, Unit circle (MathWorld)
• Flash animation for learning the unit circle 4 Mayıs 2021 tarihinde Wayback Machine sitesinde arşivlendi.
• GonioLab: Visualization of the unit circle, trigonometric and hyperbolic function

Kaynakça

• İngilizce vikipedi24 Ekim 2014 tarihinde Wayback Machine sitesinde arşivlendi.