Processo de Gram-Schmidt

Em matemática e análise numérica, o processo de Gram-Schmidt é um método para ortonormalização de um conjunto de vetores em um espaço com produto interno, normalmente o espaço euclidiano Rⁿ. O processo de Gram–Schmidt recebe um conjunto finito, linearmente independente de vetores S = {v₁, …, v_n} e retorna um conjunto ortonormal S' = {u₁, …, u_n} que gera o mesmo subespaço S inicial.

O método leva o nome de Jørgen Pedersen Gram e Erhard Schmidt, mas pode ser encontrado antes nos trabalhos de Laplace e Cauchy. Em teoria de decomposição do grupo de Lie é generalizado pela decomposição de Iwasawa.^[1]

A aplicação do processo de Gram-Schmidt aos vetores de uma coluna matricial completa de classificação produz a fatoração QR (decomposta numa matriz ortogonal e uma matriz triangular).

O processo de Gram-Schmidt

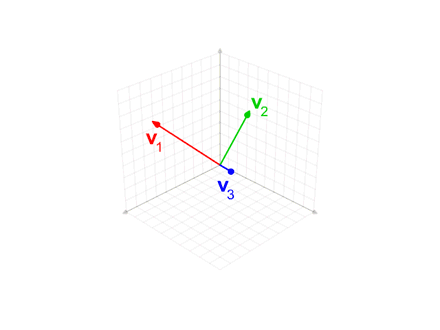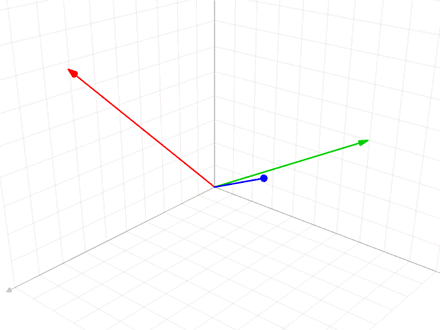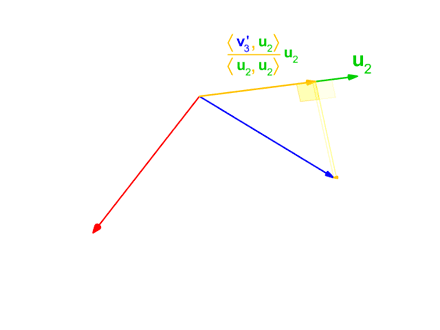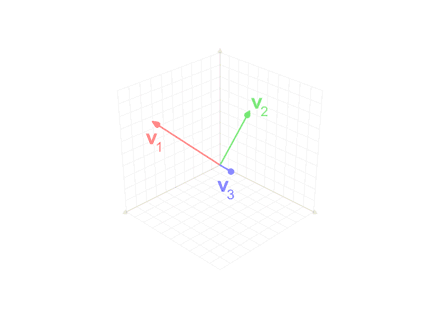
Define-se o operador projeção por:

${\displaystyle \mathrm {proj} _{\mathbf {u} }\,(\mathbf {v} )={\langle \mathbf {v} ,\mathbf {u} \rangle \over \langle \mathbf {u} ,\mathbf {u} \rangle }\mathbf {u} ,}$

no qual ${\displaystyle \langle \mathbf {v} ,\mathbf {u} \rangle }$ denota o produto interno dos vetores v e u. Esse operador projeta o vetor v ortogonalmente sobre a linha gerada pelo vetor u. Se u=0, define-se ${\displaystyle \mathrm {proj} _{0}\,(\mathbf {v} ):=0}$. i.e., o mapa projetado ${\displaystyle \mathrm {proj} _{0}}$ é o mapa zero, enviando cada vetor ao vetor zero.

O processo de Gram-Schmidt funciona então como denotado abaixo:

${\displaystyle {\begin{aligned}\mathbf {u} _{1}&=\mathbf {v} _{1},&\mathbf {e} _{1}&={\mathbf {u} _{1} \over \|\mathbf {u} _{1}\|}\\\mathbf {u} _{2}&=\mathbf {v} _{2}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{2}),&\mathbf {e} _{2}&={\mathbf {u} _{2} \over \|\mathbf {u} _{2}\|}\\\mathbf {u} _{3}&=\mathbf {v} _{3}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{3})-\mathrm {proj} _{\mathbf {u} _{2}}\,(\mathbf {v} _{3}),&\mathbf {e} _{3}&={\mathbf {u} _{3} \over \|\mathbf {u} _{3}\|}\\\mathbf {u} _{4}&=\mathbf {v} _{4}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{4})-\mathrm {proj} _{\mathbf {u} _{2}}\,(\mathbf {v} _{4})-\mathrm {proj} _{\mathbf {u} _{3}}\,(\mathbf {v} _{4}),&\mathbf {e} _{4}&={\mathbf {u} _{4} \over \|\mathbf {u} _{4}\|}\\&{}\ \ \vdots &&{}\ \ \vdots \\\mathbf {u} _{k}&=\mathbf {v} _{k}-\sum _{j=1}^{k-1}\mathrm {proj} _{\mathbf {u} _{j}}\,(\mathbf {v} _{k}),&\mathbf {e} _{k}&={\mathbf {u} _{k} \over \|\mathbf {u} _{k}\|}.\end{aligned}}}$

A sequência u₁, ..., u_k é o sistema de vetores ortogonais requerido, e o vetores normalizados e₁, ..., e_k formam um conjunto ortonormal. O cálculo da sequência u₁, ..., u_k é conhecido como ortogonalização Gram–Schmidt,enquanto o cálculo da sequência e₁, ..., e_k é conhecido como ortonormalização Gram–Schmidt, à medida que os vetores estão normalizados.

Para verificar se essas fórmulas produzem uma sequência ortogonal, primeiro calcule ‹ u₁,u₂ ›substituindo a fórmula acima por u₂: obtém-se zero. Então proceda para o cálculo de ‹ u₁,u₃ › novamente substituindo a fórmula por u₃: obtém-se mais uma vez zero. A prova geral procede por indução matemática.

Geometricamente, esse método se segue como: para calcular u_i, projeta-se v_i ortogonalmente sobre o subespaço U gerado por u₁, ..., u_i−1, que é o mesmo que o subespaço gerado por v₁, ..., v_i−1. O vetor u_i então é definido como a diferença entre v_i e essa projeção, garantido como ortogonal para todos os vetores no subespaço U.

O processo de Gram-Schmidt também se aplica a uma sequência de conjunto contável linear e independente {v_i}_i. O resultado é uma sequência ortogonal (ou ortonormal) {u_i}_i tal para número natural n: a extensão de algébrica v₁, ..., v_n é a mesma de que u₁, ..., u_n.

Se o processo de Gram-Schmidt é aplicado a uma sequência linearmente dependente, ele emite 0 vetor em ith etapa, assumindo que v_i é a combinação linear de v₁, ..., v_i−1. Se uma base ortonormal está a ser produzida, então o algoritmo deve testar para zero vetores na saída (output) e descartá-los porque nenhum múltiplo de um vetor zero pode ter um comprimento de valor 1. O número de vetores de saída dados pelo algoritmo será então a dimensão do espaço gerado pelos inputs originais.

Uma variante do processo de Gram-Schmidt utilizando indução transfinita aplicada a uma sequência infinita de vetores (possivelmente incontável) ${\displaystyle (v_{\alpha })_{\alpha <\lambda }}$ produz um conjunto de vetores ortonormais ${\displaystyle (u_{\alpha })_{\alpha <\kappa }}$ com ${\displaystyle \kappa \leq \lambda }$ de tal modo que qualquer ${\displaystyle \alpha \leq \lambda }$, o complemento do espaço de ${\displaystyle \lbrace u_{\beta }:\beta <\min(\alpha ,\kappa )\rbrace }$ é o mesmo que ${\displaystyle \lbrace v_{\beta }:\beta <\alpha \rbrace }$. Particularmente, quando aplicado a uma base (algébrica) de um espaço de Hilbert (ou, mais geralmente, uma base de qualquer subespaço denso), produz-se uma base ortonormal (analítica-funcional). Note-se que, no caso geral, muitas vezes a desigualdade estrita ${\displaystyle \kappa <\lambda }$ preserva, mesmo que o conjunto inicial for linearmente independente, e o espaço de ${\displaystyle (u_{\alpha })_{\alpha <\kappa }}$ não precisa ser um subespaço do espaço de ${\displaystyle (v_{\alpha })_{\alpha <\lambda }}$ (pelo contrário, é um subespaço de sua conclusão).

Exemplo

Considerado o seguinte conjunto de vetores em R² (com o produto interno convencional)

${\displaystyle S=\left\lbrace \mathbf {v} _{1}={\begin{pmatrix}3\\1\end{pmatrix}},\mathbf {v} _{2}={\begin{pmatrix}2\\2\end{pmatrix}}\right\rbrace .}$

Então, proceda Gram–Schmidt, a fim de obter um conjunto ortogonal de vetores:

${\displaystyle \mathbf {u} _{1}=\mathbf {v} _{1}={\begin{pmatrix}3\\1\end{pmatrix}}}$

${\displaystyle \mathbf {u} _{2}=\mathbf {v} _{2}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{2})={\begin{pmatrix}2\\2\end{pmatrix}}-\mathrm {proj} _{({3 \atop 1})}\,({{\begin{pmatrix}2\\2\end{pmatrix}})}={\begin{pmatrix}2\\2\end{pmatrix}}-{\begin{pmatrix}4/5\end{pmatrix}}{\begin{pmatrix}3\\1\end{pmatrix}}={\begin{pmatrix}-2/5\\6/5\end{pmatrix}}.}$

Verifica-se que os vetores u₁ e u₂ são de fato ortogonais:

${\displaystyle \langle \mathbf {u} _{1},\mathbf {u} _{2}\rangle =\left\langle {\begin{pmatrix}3\\1\end{pmatrix}},{\begin{pmatrix}-2/5\\6/5\end{pmatrix}}\right\rangle =-{\frac {6}{5}}+{\frac {6}{5}}=0,}$

notando que, se o produto escalar de dois vetores for 0 , então eles serão ortogonais.

Para vetores diferentes de zero, pode-se normalizar os vetores dividindo seu tamanhos como mostrado acima:${\displaystyle \mathbf {e} _{1}={1 \over {\sqrt {10}}}{\begin{pmatrix}3\\1\end{pmatrix}}}$

${\displaystyle \mathbf {e} _{2}={1 \over {\sqrt {40 \over 25}}}{\begin{pmatrix}-2/5\\6/5\end{pmatrix}}={1 \over {\sqrt {10}}}{\begin{pmatrix}-1\\3\end{pmatrix}}.}$

Estabilidade numérica

Quando esse processo é executado em um computador, os vetores ${\displaystyle \mathbf {u} _{k}}$ muitas vezes não são muito ortogonais, devido a erros de arredondamento. Para o processo de Gram-Schmidt, tal como descrito acima, (podendo ser referenciado eventualmente como "processo de Gram-Schmidt clássico") tal perda de ortogonalidade é algo particularmente ruim; Portanto, diz-se que o processo (clássico) de Gram-Schmidt é numericamente instável.

O processo de Gram-Schmidt pode ser estabilizado por meio de uma pequena modificação; tal versão do processo é por vezes referida como processo Gram-Schmidt modificado. Tal abordagem dá o mesmo resultado que a fórmula original numa aritmética exata e introduz erros menores na aritmética de finita-precisão. Ao invés de calcular o vetor u_k como

${\displaystyle \mathbf {u} _{k}=\mathbf {v} _{k}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{k})-\mathrm {proj} _{\mathbf {u} _{2}}\,(\mathbf {v} _{k})-\cdots -\mathrm {proj} _{\mathbf {u} _{k-1}}\,(\mathbf {v} _{k}),}$

ele é calculado como

${\displaystyle {\begin{aligned}\mathbf {u} _{k}^{(1)}&=\mathbf {v} _{k}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{k}),\\\mathbf {u} _{k}^{(2)}&=\mathbf {u} _{k}^{(1)}-\mathrm {proj} _{\mathbf {u} _{2}}\,(\mathbf {u} _{k}^{(1)}),\\&\,\,\,\vdots \\\mathbf {u} _{k}^{(k-2)}&=\mathbf {u} _{k}^{(k-3)}-\mathrm {proj} _{\mathbf {u} _{k-2}}\,(\mathbf {u} _{k}^{(k-3)}),\\\mathbf {u} _{k}^{(k-1)}&=\mathbf {u} _{k}^{(k-2)}-\mathrm {proj} _{\mathbf {u} _{k-1}}\,(\mathbf {u} _{k}^{(k-2)}).\end{aligned}}}$

Cada passo encontra um vetor ${\displaystyle \mathbf {u} _{k}^{(i)}}$ ortogonal a ${\displaystyle \mathbf {u} _{k}^{(i-1)}}$. Assim ${\displaystyle \mathbf {u} _{k}^{(i)}}$ também é ortogonalizado contra quaisquer erros introduzidos no cálculo de ${\displaystyle \mathbf {u} _{k}^{(i-1)}}$.

Este método é utilizado na animação anterior, quando o vetor intermediário v'₃ é usado na ortogonalização do vetor azul v₃.

Algoritmo

O algoritmo a seguir implementa a ortonormalização Gram-Schmidt estabilizada. Os vetores v₁, ..., v_k são substituídos por vetores ortonormais que abrangem o mesmo subespaço.

O custo desse algoritmo é assintoticamente 2nk² operações de ponto flutuante, nas quais n é a dimensionalidade dos vetores (Golub & Van Loan 1996, §5.2.8).

Fórmula determinante

O resultado do processo de Gram-Schmidt pode ser expresso em uma fórmula não-recursiva usando determinantes.

${\displaystyle \mathbf {e} _{j}={\frac {1}{\sqrt {D_{j-1}D_{j}}}}{\begin{vmatrix}\langle \mathbf {v} _{1},\mathbf {v} _{1}\rangle &\langle \mathbf {v} _{2},\mathbf {v} _{1}\rangle &\dots &\langle \mathbf {v} _{j},\mathbf {v} _{1}\rangle \\\langle \mathbf {v} _{1},\mathbf {v} _{2}\rangle &\langle \mathbf {v} _{2},\mathbf {v} _{2}\rangle &\dots &\langle \mathbf {v} _{j},\mathbf {v} _{2}\rangle \\\vdots &\vdots &\ddots &\vdots \\\langle \mathbf {v} _{1},\mathbf {v} _{j-1}\rangle &\langle \mathbf {v} _{2},\mathbf {v} _{j-1}\rangle &\dots &\langle \mathbf {v} _{j},\mathbf {v} _{j-1}\rangle \\\mathbf {v} _{1}&\mathbf {v} _{2}&\dots &\mathbf {v} _{j}\end{vmatrix}}}$

${\displaystyle \mathbf {u} _{j}={\frac {1}{D_{j-1}}}{\begin{vmatrix}\langle \mathbf {v} _{1},\mathbf {v} _{1}\rangle &\langle \mathbf {v} _{2},\mathbf {v} _{1}\rangle &\dots &\langle \mathbf {v} _{j},\mathbf {v} _{1}\rangle \\\langle \mathbf {v} _{1},\mathbf {v} _{2}\rangle &\langle \mathbf {v} _{2},\mathbf {v} _{2}\rangle &\dots &\langle \mathbf {v} _{j},\mathbf {v} _{2}\rangle \\\vdots &\vdots &\ddots &\vdots \\\langle \mathbf {v} _{1},\mathbf {v} _{j-1}\rangle &\langle \mathbf {v} _{2},\mathbf {v} _{j-1}\rangle &\dots &\langle \mathbf {v} _{j},\mathbf {v} _{j-1}\rangle \\\mathbf {v} _{1}&\mathbf {v} _{2}&\dots &\mathbf {v} _{j}\end{vmatrix}}}$

na qual D ₀=1 e, para j ≥ 1, D _j é o determinante Gram

${\displaystyle D_{j}={\begin{vmatrix}\langle \mathbf {v} _{1},\mathbf {v} _{1}\rangle &\langle \mathbf {v} _{2},\mathbf {v} _{1}\rangle &\dots &\langle \mathbf {v} _{j},\mathbf {v} _{1}\rangle \\\langle \mathbf {v} _{1},\mathbf {v} _{2}\rangle &\langle \mathbf {v} _{2},\mathbf {v} _{2}\rangle &\dots &\langle \mathbf {v} _{j},\mathbf {v} _{2}\rangle \\\vdots &\vdots &\ddots &\vdots \\\langle \mathbf {v} _{1},\mathbf {v} _{j}\rangle &\langle \mathbf {v} _{2},\mathbf {v} _{j}\rangle &\dots &\langle \mathbf {v} _{j},\mathbf {v} _{j}\rangle \end{vmatrix}}.}$

Note que a expressão para u_k é um determinante "formal", i.e. a matriz contém ambos os escalares e vetores; o significado dessa expressão é definido como sendo o resultado de um cofator de expansão ao longo da linha de vetores.

A fórmula determinante de Gram-Schmidt é computacionalmente mais lenta (exponencialmente mais lenta) do que os algoritmos recursivos descritos acima; é principalmente de interesse teórico.

Alternativas

Outros algoritmos de ortogonalização utilizam a transformação de Householder ou a rotação de Givens. Os algoritmos que utilizam a transformação de Householder são mais estáveis que o processo de Gram–Schmidt estabilizado. Por outro lado, o referido processo produz o ${\displaystyle j}$th vetor ortogonalizado baseado na interação ${\displaystyle j}$th, enquanto a ortogonalização utilizando a reflexão Householder produz todos os vetores apenas no final. Isso torno o processo de Gram–Schmidt aplicável ao método iterativo assim como a iteração Arnoldi.

Outra alternativa é motivada ainda pelo uso da decomposição de Cholesky para invertendo a matriz das equações normais de mínimos quadrados lineares. Tome-se ${\displaystyle \mathbf {V} }$ a estar num posto coluna cheia de uma matriz, cujas colunas precisam ser ortogonalizadas. A matriz ${\displaystyle \mathbf {V} ^{*}\mathbf {V} }$ é uma matriz transposta conjugada e definida positiva, de tal modo que possa ser escrita ${\displaystyle \mathbf {V} ^{*}\mathbf {V} =\mathbf {L} \mathbf {L} ^{*},}$ utilizando a decomposição de Cholesky. A matriz triangular inferior ${\displaystyle \mathbf {L} }$ com entradas diagonais estritamente positivas é inversa. As colunas da matriz ${\displaystyle \mathbf {U} =\mathbf {V} (\mathbf {L} ^{-1})^{*}}$ são ortonormais e abrangem o mesmo subespaço como as colunas da matriz original ${\displaystyle \mathbf {V} }$. O uso explícito do conteúdo ${\displaystyle \mathbf {V} ^{*}\mathbf {V} }$ torna o algoritmo instável, espacialmente se o produto do número de condicionamento for elevado. No entanto, esse algoritmo é utilizado na prática e implementado em alguns pacotes de software por conta de sua alta eficiência e simplicidade.

Em mecânica quântica existem vários esquemas de ortogonalização com características mais adequadas para certas aplicações do que os de Gram-Schmidt. No entanto, o Gram-Schmidt continua a ser um algoritmo popular e eficaz, mesmo para os maiores cálculos de estrutura eletrônica.^[2]

Referências

Leituras adicionais

• Bau III, David; Trefethen, Lloyd N. (1997), Numerical linear algebra, ISBN 978-0-89871-361-9, Philadelphia: Society for Industrial and Applied Mathematics .
• Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations, ISBN 978-0-8018-5414-9 3rd ed. , Johns Hopkins .
• Greub, Werner (1975), Linear Algebra 4th ed. , Springer .
• Soliverez, C. E.; Gagliano, E. (1985), «Orthonormalization on the plane: a geometric approach» (PDF), Mex. J. Phys., 31 (4): 743-758 .

Ligações externas

• Hazewinkel, Michiel, ed. (2001), «Orthogonalization», Enciclopédia de Matemática, ISBN 978-1-55608-010-4 (em inglês), Springer 
• Harvey Mudd College Math Tutorial on the Gram-Schmidt algorithm
• Earliest known uses of some of the words of mathematics: G The entry "Gram-Schmidt orthogonalization" has some information and references on the origins of the method.
• Demonstrações: Gram Schmidt process in plane e Gram Schmidt process in space
• Gram-Schmidt orthogonalization applet
• NAG Gram–Schmidt orthogonalization of n vectors of order m routine
• Prova: Raymond Puzio, Keenan Kidwell. "proof of Gram-Schmidt orthogonalization algorithm" (version 8). PlanetMath.org.