Integral de superfície

Uma integral de superfície é uma generalização das integrais múltiplas sobre uma superfície.^[1][2][3] Dada uma superfície S, pode-se integrar sobre ela um campo escalar ou um campo vetorial. Aplicações de integrais de superfícies aparecem em vários ramos da ciência e das engenharias, tais como em problemas envolvendo fluxo de fluido e de calor, eletricidade, magnetismo, massa e centro de gravidade.^[4] Por exemplo, ao integrarmos uma função densidade de massa sobre uma superfície, obteremos a massa aplicada sobre a superfície.^[2] Em uma superfície orientável, a integral de superfície do produto interno de um campo vetorial pelo campo normal à superfície fornece o fluxo desse campo, indicado por pela letra grega maiúscula Φ.^[3]

Definição

Seja ${\displaystyle g:\mathbb {R} ^{3}\to \mathbb {R} }$, ${\displaystyle g=g(x,y,z)}$, uma função definida em todos os pontos de uma superfície ${\displaystyle S}$. A integral de superfície de ${\displaystyle g}$ sobre ${\displaystyle S}$ é definida por^[2]:

$${\displaystyle \int \int _{S}gd\sigma }$$

onde, ${\displaystyle d\sigma }$ é o elemento infinitesimal de área sobre a superfície.

Se ${\displaystyle S}$ é uma superfície orientável, então definimos a integral de superfície de um campo vetorial ${\displaystyle F}$ sobre ${\displaystyle S}$ por^[3]:

$${\displaystyle \int \int _{S}\mathbf {F} \cdot \mathbf {n} d\sigma }$$

onde, ${\displaystyle \mathbf {n} }$ é o campo normal escolhido na orientação da superfície. O integrando na forma de produto escalar evidencia que somente as componentes do campo perpendiculares à superfície ${\displaystyle S}$ contribuirão no cálculo do fluxo.^[4]

Orientação

Assim como as curvas, também as superfícies precisam ser orientadas, a fim de que, ao adotar certa convenção, sempre se encontre o mesmo sinal para fluxo Φ. Diz-se que uma superfície de dois lados é orientável e que uma superfície de um único lado é não orientável. Assim, existe a necessidade de distinção dos lados de uma superfície orientável e convenção para orientação considerada positiva e negativa, pois ao inverter a orientação de S inverte-se o sinal de Φ.^[4]

Sendo assim:

O sinal de ${\displaystyle {\overrightarrow {n}}}$ serve para orientar ${\displaystyle S}$.

Para o cálculo de ${\displaystyle {\overrightarrow {n}}}$:
Suponha que a superfície ${\displaystyle S}$ seja dada como: ${\displaystyle z=g(x,y)}$ ou ${\displaystyle y=g(x,z)}$ ou ${\displaystyle x=g(y,z)}$.
Reescrevendo cada uma das equações na forma ${\displaystyle G(x,y,z)=0}$ é possível interpretar a última como a equação de uma superfície de nível de uma função ${\displaystyle w=G(x,y,z)}$.
A partir do conceito que ${\displaystyle {\overrightarrow {\nabla }}G}$ é um vetor 3-D e representa um vetor normal à superfície de nível ${\displaystyle G(x,y,z)=0}$, pode-se definir ${\displaystyle {\overrightarrow {n}}}$ da seguinte forma:

${\displaystyle {\overrightarrow {n}}={\frac {{\overrightarrow {\nabla }}G}{|{\overrightarrow {\nabla }}G|}}}$ ou ${\displaystyle {\overrightarrow {n}}=-{\frac {{\overrightarrow {\nabla }}G}{|{\overrightarrow {\nabla }}G|}}}$

Elemento de área

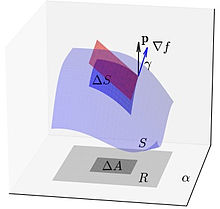
O cálculo do elemento infinitesimal de área sobre a superfície pode ser feito com o auxílio de uma projeção adequada da superfície ${\textstyle S}$ sobre um plano do espaço cartesiano. Suponhamos que ${\textstyle S}$ é descrita pela superfície de nível ${\displaystyle f(x,y,z)=c}$. Consideremos, ainda, um plano dado ${\textstyle \alpha }$ de normal unitária ${\displaystyle \mathbf {p} }$. A projeção de ${\displaystyle S}$ sobre ${\displaystyle \alpha }$ define uma região planar que denotaremos por ${\textstyle R}$.

Com isso, aproximamos um elemento de área ${\displaystyle \Delta S}$ da superfície ${\displaystyle S}$ pela área do elemento tangente associado. Este, por sua vez, pode ser calculado em função do elemento de área ${\displaystyle \Delta S}$ projetado sobre o plano ${\displaystyle \alpha }$. Denotando este por ${\displaystyle \Delta A}$, temos^[2]:

$${\displaystyle \Delta S\approx {\frac {1}{|\cos \gamma |}}\Delta A}$$

onde, ${\displaystyle \gamma }$ é o ângulo entre o vetor gradiente ${\displaystyle \nabla f}$ e o vetor ${\displaystyle \mathbf {p} }$ calculado em algum ponto de ${\displaystyle \Delta S}$.

Assim, podemos calcular o elemento de área ${\displaystyle d\sigma }$ por^[2]:

$${\displaystyle d\sigma ={\frac {1}{|\cos \gamma |}}dA}$$

onde, ${\displaystyle \gamma }$ é o ângulo entre o vetor gradiente ${\displaystyle \nabla f}$ e o vetor ${\displaystyle \mathbf {p} }$. ${\displaystyle dA}$ é o elemento de área planar.

Observamos, ainda, que o ângulo ${\displaystyle \gamma }$ está relacionado ao produto interno entre ${\displaystyle \nabla f}$ e ${\displaystyle \mathbf {p} }$ por:

$${\displaystyle \nabla f\cdot \mathbf {p} =|\nabla f||\mathbf {p} |\cos \gamma }$$

Segue, daí, que o elemento de área ${\displaystyle d\sigma }$ pode ser calculado por:

$${\displaystyle d\sigma ={\frac {|\nabla f||\mathbf {p} |}{|\nabla f\cdot \mathbf {p} |}}dA}$$

Teorema

Seja ${\displaystyle S}$ uma superfície suave da forma ${\displaystyle z=g(x,y)}$ ou ${\displaystyle y=g(x,z)}$ ou ${\displaystyle x=g(y,z)}$ e seja ${\displaystyle {\overrightarrow {F}}}$ um campo vetorial contínuo em ${\displaystyle S}$. Supondo também que a equação de ${\displaystyle S}$ seja reescrita como ${\displaystyle G(x,y,z)=0}$, ao passar ${\displaystyle g}$ para o membro esquerdo da equação e seja ${\displaystyle R}$ a projeção de ${\displaystyle S}$ no plano coordenado das variáveis independentes de ${\displaystyle g}$.^[4] Então:

$${\displaystyle \phi =\int \int _{S}{\overrightarrow {F}}\bullet {\overrightarrow {n}}dS=\pm \int \int _{R}{\overrightarrow {F}}\bullet {\overrightarrow {\nabla }}GdA}$$

Cálculo da integral de superfície

Com base no cálculo do elemento de área sobre uma superfície podemos calcular a integral de superfície como uma integral dupla sobre uma região planar.^[2] Seja ${\displaystyle g:\mathbb {R} ^{3}\to \mathbb {R} }$, ${\displaystyle g=g(x,y,z)}$, uma função definida em todos os pontos de uma superfície ${\displaystyle S}$ descrita pela superfície de nível ${\displaystyle f(x,y,z)=c}$. Seja, ainda, ${\displaystyle R}$ a região planar definida pela projeção de ${\displaystyle S}$ sobre um plano dado ${\displaystyle \alpha }$. Então, a integral de superfície de ${\displaystyle g}$ sobre ${\displaystyle S}$ pode ser calculada pela seguinte integral dupla sobre ${\displaystyle R}$:

$${\displaystyle \int \int _{S}gd\sigma =\int \int _{R}g{\frac {|\nabla f||\mathbf {p} |}{|\nabla f\cdot \mathbf {p} |}}dA}$$

Observações Importantes

• Já que foi feita substituição de uma integração de superfície por uma integração dupla na região dos planos coordenados, o integrando deve coincidir com os pontos da superfície. É indispensável identificar a superfície.^[4]

• Nas aplicações, as superfícies mais simples são os planos, cúbicas, e os tetraedros. Também é possível ter superfícies de revolução, como cilíndricas, e superfícies quádricas.^[4]

• É importante a observação do integrando ${\displaystyle {\overrightarrow {F}}\bullet {\overrightarrow {\nabla }}G}$, para escolha do sistema de coordenadas mais apropriado, tendo em vista a simetria da superfície.^[4]

Exemplo

Exemplo da apostila da prof Irene Strauch^[4].

• Calcular o fluxo de ${\displaystyle {\overrightarrow {F}}=3z^{2}{\overrightarrow {i}}+6{\overrightarrow {j}}+6xz{\overrightarrow {k}}}$ através da superfície ${\displaystyle S}$ dada por ${\displaystyle y=x^{2}}$ com ${\displaystyle 0\leq x\leq 2}$ e ${\displaystyle 0\leq z\leq 3}$ e orientada para fora da concavidade.

Resolução

${\displaystyle G(x,y,z)=y-f(x,z)=y-x^{2}}$
${\displaystyle {\overrightarrow {\nabla }}G(x,y,z)=-2x{\overrightarrow {i}}+{\overrightarrow {j}}}$
${\displaystyle {\overrightarrow {F}}\bullet {\overrightarrow {\nabla }}G=-6xz^{2}+6}$
A região projetada é o retângulo no plano ${\displaystyle xz}$ restrito a ${\displaystyle 0\leq x\leq 2}$ e ${\displaystyle 0\leq z\leq 3}$, então
${\displaystyle \phi =\int \int _{R}(-6xz^{2}+6)dA}$
${\displaystyle \phi =-\int _{0}^{3}\int _{0}^{2}(-6xz^{2}+6)dxdz}$
${\displaystyle \phi =-36+(4\cdot 27)=72}$

Integral de superfície de campos escalares

Supondo que f seja uma função de um campo escalar de três variáveis em uma superfície suave S. Para encontrar uma fórmula explícita da integral de superficie f sobre S, é precido parametrizar S. Dada a parametrização r(s, t), onde (s, t) varia em alguma região T no plano, a integral de superfície é definida por:

${\displaystyle \iint _{S}f\,\mathrm {d} S=\iint _{T}f(\mathbf {r} (s,t))\left\|{\partial \mathbf {r} \over \partial s}\times {\partial \mathbf {r} \over \partial t}\right\|\mathrm {d} s\,\mathrm {d} t}$

Se S for o gráfico de uma função ${\displaystyle z=z(x,y)}$, então:

${\displaystyle {\begin{aligned}\iint _{S}f\,\mathrm {d} S&{}=\iint _{T}f\mathbf {(} x,y,z(x,y)){\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,\mathrm {d} x\,\mathrm {d} y\end{aligned}}}$

Onde T é a projeção de S sobre o plano xy.^[5]

Integral de superfície de campos vetoriais

Seja uma superfície suave ${\displaystyle S}$ representada por ${\displaystyle {\vec {r}}(u,v)=x(u,v){\vec {i}}+y(u,v){\vec {j}}+z(u,v){\vec {k}}}$ e ${\displaystyle {\vec {n}}={\vec {n}}(u,v)}$ um vetor unitário normal a essa superfície. Dado um campo vetorial ${\displaystyle {\vec {f}}}$ definido sobre ${\displaystyle S}$, a integral de superfície é definida por:

${\displaystyle {\begin{aligned}\iint _{S}\left({\mathbf {\vec {f}} }\cdot {\mathbf {\vec {n}} }\right)\,\mathrm {d} s\ =\iint _{T}{\mathbf {\vec {f}} }(\mathbf {\vec {r}} (s,t))\cdot {\vec {n}}(s,t)\left\|{\frac {\partial \mathbf {r} }{\partial s}}\times {\frac {\partial \mathbf {r} }{\partial t}}\right\|\mathrm {d} s\,\mathrm {d} t\end{aligned}}}$

quando a integral da direita existe. Se ${\displaystyle S}$ é suave por partes, a integral é definida sobre a soma das integrais de cada fragmento de ${\displaystyle S}$. Como o vetor unitário ${\displaystyle {\vec {n}}}$ é dado por:

${\displaystyle {\begin{aligned}{\vec {n}}={{\frac {\partial \mathbf {r} }{\partial s}}\times {\frac {\partial \mathbf {r} }{\partial t}} \over \left\|{\frac {\partial \mathbf {r} }{\partial s}}\times {\frac {\partial \mathbf {r} }{\partial t}}\right\|}\end{aligned}}}$

os módulos do produto vetorial se anulam. A expressão se torna:

${\displaystyle {\begin{aligned}\iint _{S}\left({\mathbf {\vec {f}} }\cdot {\mathbf {\vec {n}} }\right)\,\mathrm {d} s\ =\pm \iint _{T}{\mathbf {\vec {f}} }(\mathbf {\vec {r}} (s,t))\left({\frac {\partial \mathbf {r} }{\partial s}}\times {\frac {\partial \mathbf {r} }{\partial t}}\right)\mathrm {d} s\,\mathrm {d} t\end{aligned}}}$

A integral terá sinal positivo se o lado de ${\displaystyle S}$ escolhido para integração for o lado do qual emana o vetor unitário ${\displaystyle {\vec {n}}}$. Do contrário, o sinal será negativo.^[5]

Aplicações

Aplicações de integrais de superfícies aparecem em vários ramos da ciência e das engenharias. Aqui, discutimos rapidamente algumas delas.
Na Mecânica dos Fluidos poderemos ter fluxo de um campo de velocidades ${\displaystyle {\vec {v}}}$. No Eletromagnetismo teremos fluxo de um campo elétrico ${\displaystyle {\vec {E}}}$ ou de um campo de indução magnética ${\displaystyle {\vec {B}}}$ através de uma superfície ${\displaystyle S}$. Se o campo vetorial for um campo de densidade de corrente, indicado pela letra ${\displaystyle {\vec {J}}}$, então o fluxo terá dimensão de massa por unidade de tempo ou de corrente elétrica, conforme estejamos estudando o movimento de um fluido ou o movimento de cargas elétricas, respectivamente.^[4]

Massa

Suponhamos que ${\displaystyle S:f(x,y,z)=c}$ descreve a superfície de uma placa fina com densidade de massa dada pela função ${\displaystyle \delta =\delta (x,y,z)}$. Então, a massa ${\displaystyle M}$ da placa é dada pela integral de superfície^[2]:

$${\displaystyle M=\int \int gd\sigma }$$

.

Fluxo

Seja ${\displaystyle S:f(x,y,z)=c}$ uma superfície no espaço e ${\displaystyle {\vec {F}}}$ um campo vetorial. Em cada ponto de S existem dois vetores normais unitários, apontando em direções opostas; o vetor normal unitário com orientação positiva, denotado por ${\displaystyle {\hat {n}}}$. Se S é uma superfície fechada, como uma esfera ou um cubo, então por convenção ela é orientada de forma que o lado exterior seja o positivo(${\displaystyle {\hat {n}}}$sempre aponta pra fora de S).^[6]

Então o fluxo através de S é determinado por

$${\displaystyle \iint \limits _{S}{\vec {F}}\cdot {\hat {n}}dS}$$

onde ${\displaystyle dS}$ é o elemento de área da superfície

Também é usada a notação ${\displaystyle {\vec {dS}}={\hat {n}}dS}$

Por exemplo, se ${\displaystyle {\vec {F}}}$ é o campo de velocidades de um escoamento, então esta integral fornece o fluxo do escoamento através de ${\displaystyle S}$.^[2]

Ver também

• Teorema de Stokes
• Teorema de Gauss

Referências