Bètaverdeling

Bèta
kansdichtheid
Verdelingsfunctie
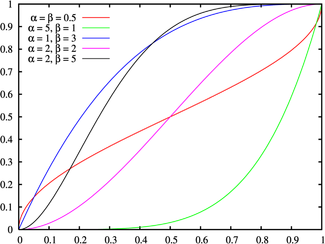Parameters	${\displaystyle \alpha >0}$ ${\displaystyle \beta >0}$
Drager	${\displaystyle x\in [0;1]}$
kansdichtheid	${\displaystyle {\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}}$
Verdelingsfunctie	Niet expliciet op te schrijven
Verwachtingswaarde	${\displaystyle {\frac {\alpha }{\alpha +\beta }}}$
Modus	${\displaystyle {\frac {\alpha -1}{\alpha +\beta -2}}}$ als ${\displaystyle \alpha >1,\beta >1}$
Variantie	${\displaystyle {\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}}$
Scheefheid	${\displaystyle {\frac {2\,(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}}$
Entropie	${\displaystyle \ln \mathrm {\mathrm {B} } (a,b)-(a-1)\psi (a)-}$ ${\displaystyle (b-1)\psi (b)+(a+b-2)\psi (a+b)}$
Moment- genererende functie	${\displaystyle 1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {t^{k}}{k!}}}$
Portaal    Wiskunde

In de kansrekening en statistiek is de bètaverdeling een continue kansverdeling, met twee parameters. De bètaverdeling wordt gebruikt om de kansverdeling van gesorteerde grootheden te beschrijven. Tevens wordt de bètaverdeling uitgebreid gebruikt in de Bayesiaanse statistiek vanwege handige wiskundige eigenschappen van deze verdeling.

Definitie

De kansdichtheid van de bètaverdeling is gedefinieerd op het interval [0, 1] als

${\displaystyle f(x;\alpha ,\beta )={\frac {1}{\mathrm {B} (\alpha ,\beta )}}x^{\alpha -1}(1-x)^{\beta -1}}$

Daarin zijn ${\displaystyle \alpha }$ en ${\displaystyle \beta }$ beide positieve reële getallen en is

${\displaystyle \mathrm {B} (\alpha ,\beta )={\frac {\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}}}$

de bètafunctie.

Vorm van de grafiek

De bètaverdeling is gedefinieerd op het interval [0, 1]. De vorm van de grafiek hangt af van de parameters:

• Als ${\displaystyle \alpha =\beta }$, dan is de grafiek symmetrisch rond 1/2
• ${\displaystyle \alpha <1,\ \beta <1}$: de grafiek heeft een U-vorm (rode lijn)
• ${\displaystyle \alpha <1,\ \beta \geq 1}$: de grafiek is dalend (blauwe lijn)
• ${\displaystyle \alpha =1,\ \beta =1}$: deze bètaverdeling is de uniforme verdeling
• ${\displaystyle \alpha >1,\ \beta \leq 1}$: de grafiek is stijgend (groene lijn)
• ${\displaystyle \alpha >1,\ \beta >1}$: de grafiek is unimodaal (heeft 1 modus) (paarse en zwarte lijn)

Verwantschap met andere verdelingen

• De bèta${\displaystyle (1,1)}$-verdeling is gelijk aan de continue uniforme verdeling.
• Als ${\displaystyle X}$ en ${\displaystyle Y}$ onafhankelijk zijn en respectievelijk een ${\displaystyle \gamma (a,c)}$- en ${\displaystyle \gamma (b,c)}$-verdeling hebben, dan heeft ${\displaystyle X/(X+Y)}$ een bèta${\displaystyle (a,c)}$-verdeling