離散時間フーリエ変換 (りさんじかんフーリエへんかん、英 : Discrete-time Fourier transform 、DTFT )はフーリエ変換 の一種。したがって、通常時間領域 の関数を周波数領域 に変換する。ただし、DTFTでは元の関数は離散的 でなければならない。そのような入力は連続関数の標本化 によって生成される。
DTFTの周波数領域の表現は常に周期的関数である。したがって1つの周期に必要な情報が全て含まれるため、DTFTを「有限な」周波数領域への変換であるということもある。
定義 実数または複素数の離散集合 x [ n ] , n ∈ Z {\displaystyle x[n],\;n\in \mathbb {Z} } 整数 )が与えられたとき、 x [ n ] {\displaystyle x[n]\,} 離散時間フーリエ変換 (DTFT)は次にように表される。
X ( ω ) = ∑ n = − ∞ ∞ x [ n ] e − i ω n {\displaystyle X(\omega )=\sum _{n=-\infty }^{\infty }x[n]\,e^{-i\omega n}}
標本化との関係 名称が暗に示している通り、{x[n]} は連続時間関数 x ( t ) {\displaystyle x(t)\,} T {\displaystyle T\,} t = n T {\displaystyle t=nT\quad } 1 / T = f s {\displaystyle 1/T=f_{s}\,} サンプリング周波数 となる。DTFTは次の連続時間フーリエ変換 の近似である。
X ( f ) = ∫ − ∞ ∞ x ( t ) ⋅ e − i 2 π f t d t {\displaystyle X(f)=\int _{-\infty }^{\infty }x(t)\cdot e^{-i2\pi ft}\,dt}
標本化定理 で示されるように、次のくし型関数 の変調に x ( n T ) {\displaystyle x(nT)\,}
Δ T ( t ) = T ∑ n = − ∞ ∞ δ ( t − n T ) {\displaystyle \Delta _{T}(t)=T\sum _{n=-\infty }^{\infty }\delta (t-nT)\ }
その場合得られる関数のフーリエ変換は、 f s {\displaystyle f_{s}\,} X ( f ) {\displaystyle X(f)\,}
X T ( f ) = ∑ k = − ∞ ∞ X ( f − k f s ) {\displaystyle X_{\mathrm {T} }(f)=\sum _{k=-\infty }^{\infty }X(f-{kf_{s}})}
以下で示すように、これは周期関数のDTFTである。そして、ある明白な条件下で、k=0 の項はほとんど全く他の項からの歪み(折り返し雑音 )が観測されない。変調されたくし型関数は次の通りである。
x T ( t ) = T ∑ n = − ∞ ∞ x ( n T ) δ ( t − n T ) {\displaystyle x_{\mathrm {T} }(t)=T\sum _{n=-\infty }^{\infty }x(nT)\,\delta (t-nT)}
したがって、
X T ( f ) {\displaystyle X_{\mathrm {T} }(f)\,} = ∫ − ∞ ∞ [ T ∑ n = − ∞ ∞ x ( n T ) δ ( t − n T ) ] e − i 2 π f t d t {\displaystyle =\int _{-\infty }^{\infty }\left[T\sum _{n=-\infty }^{\infty }x(nT)\,\delta (t-nT)\right]e^{-i2\pi ft}\,dt} = ∑ n = − ∞ ∞ T ⋅ x ( n T ) ∫ − ∞ ∞ [ δ ( t − n T ) ⋅ e − i 2 π f t ] d t {\displaystyle =\sum _{n=-\infty }^{\infty }T\cdot x(nT)\int _{-\infty }^{\infty }\left[\delta (t-nT)\cdot e^{-i2\pi ft}\right]\,dt} = ∑ n = − ∞ ∞ T ⋅ x ( n T ) ⋅ e − i 2 π f n T {\displaystyle =\sum _{n=-\infty }^{\infty }T\cdot x(nT)\cdot e^{-i2\pi fnT}\,}
このとき次が成り立つ。
x [ n ] = T ⋅ x ( n T ) {\displaystyle x[n]=T\cdot x(nT)\,} ω = 2 π f T = 2 π ( f f s ) {\displaystyle \omega =2\pi fT=2\pi \left({\frac {f}{f_{s}}}\right)\,}
つまり X T ( f ) {\displaystyle X_{\mathrm {T} }(f)\,} X ( ω ) {\displaystyle X(\omega )\,}
ここで、 f {\displaystyle f\,} f s {\displaystyle f_{s}\,} f / f s {\displaystyle f/f_{s}\,} ω {\displaystyle \omega \,} 2 π {\displaystyle 2\pi } X ( ω ) {\displaystyle X(\omega )} 2 π {\displaystyle 2\pi }
周期性 x ( t ) {\displaystyle x(t)\,} f {\displaystyle f\,} f s {\displaystyle f_{s}\,} f / f s {\displaystyle f/f_{s}\,} 1 {\displaystyle 1} ω {\displaystyle \omega \,} 2 π {\displaystyle 2\pi } e − i ω n {\displaystyle e^{-i\omega n}\,}
e − i ( ω + 2 π k ) n = e − i ω n {\displaystyle e^{-i(\omega +2\pi k)n}=e^{-i\omega n}\,}
であり、ここで n と k は任意の整数である。したがって、
X ( ω + 2 π k ) = X ( ω ) {\displaystyle X(\omega +2\pi k)=X(\omega )\,}
となる。DTFT X ( ω ) {\displaystyle X(\omega )\,} X ( e i ω ) {\displaystyle X(e^{i\omega })\,}
周期性を強調している。 DTFT とその元になっている x ( t ) {\displaystyle x(t)\,} X ( f ) {\displaystyle X(f)\,} X ( ω ) {\displaystyle X(\omega )\,} DTFT とZ変換 との関係を強調している。 ただし、実際に周波数領域の手法でDTFTを形成したとき、その類似性は不明瞭となる。したがって、下表でも使われている通り X ( ω ) {\displaystyle X(\omega )\,}
逆変換 以下の逆変換は離散時間のシーケンスを回復させる。
x [ n ] {\displaystyle x[n]\,} = 1 2 π ∫ − π π X ( ω ) ⋅ e i ω n d ω {\displaystyle ={\frac {1}{2\pi }}\int _{-\pi }^{\pi }X(\omega )\cdot e^{i\omega n}\,d\omega } = T ∫ − 1 2 T 1 2 T X T ( f ) ⋅ e i 2 π f n T d f {\displaystyle =T\int _{-{\frac {1}{2T}}}^{\frac {1}{2T}}X_{T}(f)\cdot e^{i2\pi fnT}\,df}
積分区間はDTFTの一周期全体であり、これは {x[n]} の標本群がDTFTのフーリエ級数 展開の係数でもあることを示している。無限区間の積分では、この変換が通常のフーリエ変換 の逆変換となり、ディラックのインパルスも復元する。すなわち次のようになる。
∫ − ∞ ∞ X T ( f ) ⋅ e i 2 π f t d f = x T ( t ) = ∑ n = − ∞ ∞ x [ n ] ⋅ δ ( t − n T ) {\displaystyle \int _{-\infty }^{\infty }X_{T}(f)\cdot e^{i2\pi ft}\,df\ =\ x_{T}(t)\ =\ \sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)}
有限長シーケンス DTFTの数値的評価では、有限長のシーケンスが明らかに必要とされる。実際、長いシーケンスは矩形窓関数 で修正され、次のようになる。
X ( ω ) = ∑ n = 0 L − 1 x [ n ] e − i ω n {\displaystyle X(\omega )=\sum _{n=0}^{L-1}x[n]\,e^{-i\omega n}\,} L {\displaystyle L\,}
これは、修正前のシーケンスのスペクトルの便利な近似として使われる。これによって解像度が悪くなるが、L を増やすことで改善される。
X ( ω ) {\displaystyle X(\omega )} ( N ) {\displaystyle (N)}
ω k = 2 π N k {\displaystyle \omega _{k}={\frac {2\pi }{N}}k\,} k = 0 , 1 , … , N − 1 {\displaystyle k=0,1,\dots ,N-1\,}
これにより、次が得られる。
X [ k ] = X ( ω k ) = ∑ n = 0 L − 1 x [ n ] e − i 2 π k N n {\displaystyle X[k]=X(\omega _{k})=\sum _{n=0}^{L-1}x[n]\,e^{-i2\pi {\frac {k}{N}}n}}
N ≥ L {\displaystyle N\geq L\,}
このように変形すると、 X [ k ] {\displaystyle X[k]\,} 離散フーリエ変換 (DFT)となる。 N {\displaystyle N} L {\displaystyle L} N > L {\displaystyle N>L} 高速フーリエ変換 アルゴリズムを利用できるためである。そのことを強調する場合、「ゼロパディングDFT」あるいは「内挿DFT」と呼ぶ。しかし、値がゼロの項を使わずに単純に計算しても全く同じDFTが得られる。 N < L {\displaystyle N<L}
N > L {\displaystyle N>L}
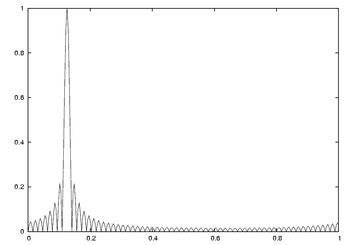
x [ n ] = e i 2 π 1 8 n {\displaystyle x[n]=e^{i2\pi {\frac {1}{8}}n}} L = 64 {\displaystyle L=64}
下に示した2つの図は、ラベルで示される通り、異なるサイズのDFTを図示したものである。どちらの場合も支配的な周波数成分は f = 1 8 = 0.125 {\displaystyle f={\begin{matrix}{\frac {1}{8}}\end{matrix}}=0.125\,} L = 64 {\displaystyle L=64} スペクトル漏れ である。左側の図がこのようになっているのは、右の図のゼロと交差している点と標本化した点が重なっている結果である。これは、有限長シーケンスのDTFTというよりも、無限に続く正弦波のような印象を与える。このような図になる原因は、矩形窓関数の使用と、64個の標本あたり8個という整数個の周期になるような周波数を選択しているためである( 1 8 = 8 64 {\displaystyle {\begin{matrix}{\frac {1}{8}}\end{matrix}}={\begin{matrix}{\frac {8}{64}}\end{matrix}}}
L = 64 および N = 64 についての DFT L = 64 および N = 256 についての DFT
他のフーリエ変換との違い 基本的にDTFTはフーリエ級数 の逆であり、後者は継続的だが、周期的入力と離散スペクトルを持っている。これら2つの変換の応用は全く異なる。
DFT と DTFT は、標準の連続フーリエ変換を離散的データに適用しようとして自然に生まれたと見ることもできる。そういった観点では、単に入力形式が異なるだけで、変換そのものは同じである。
入力が離散的なら、フーリエ変換は DTFT となる。 入力が周期的なら、フーリエ変換はフーリエ級数となる。 入力が離散的かつ周期的なら、フーリエ変換は DFT となる。 Z変換との関係 DTFT はZ変換 の特殊ケースである。両側Z変換は次のように定義される。
X ( z ) = ∑ n = − ∞ ∞ x [ n ] z − n {\displaystyle X(z)=\sum _{n=-\infty }^{\infty }x[n]\,z^{-n}}
DTFT は z = e i ω {\displaystyle z=e^{i\omega }\,} | e i ω | = 1 {\displaystyle |e^{i\omega }|=1\,} 複素平面 での単位円 付近でのZ変換 の評価である。
離散時間フーリエ変換表 下表は典型的な変換を示したものである。
n {\displaystyle n\!} ω {\displaystyle \omega \!} ( − π , π ) {\displaystyle (-\pi ,\ \pi )} それ以外 ( | ω | > π ) {\displaystyle (|\omega |>\pi \,)} X ( ω + 2 π k ) = X ( ω ) {\displaystyle X(\omega +2\pi k)=X(\omega )\,} u [ n ] {\displaystyle u[n]\!} 単位ステップ関数 である。 sinc ( t ) {\displaystyle \operatorname {sinc} (t)\!} Sinc関数 である。 δ ( ω ) {\displaystyle \delta (\omega )\!} ディラックのデルタ関数 である。 δ [ n ] {\displaystyle \delta [n]\!} クロネッカーのデルタ δ n , 0 {\displaystyle \delta _{n,0}\!} rect ( t ) {\displaystyle \operatorname {rect} (t)} t に関する次のような矩形関数 である。 r e c t ( t ) = ⊓ ( t ) = { 0 if | t | > 1 2 1 2 if | t | = 1 2 1 if | t | < 1 2 {\displaystyle \mathrm {rect} (t)=\sqcap (t)={\begin{cases}0&{\mbox{if }}|t|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}}&{\mbox{if }}|t|={\frac {1}{2}}\\[3pt]1&{\mbox{if }}|t|<{\frac {1}{2}}\end{cases}}} tri ( t ) {\displaystyle \operatorname {tri} (t)} t に関する次のような三角形関数 である。 tri ( t ) = ∧ ( t ) = { 1 + t ; − 1 ≤ t ≤ 0 1 − t ; 0 < t ≤ 1 0 otherwise {\displaystyle \operatorname {tri} (t)=\land (t)={\begin{cases}1+t;&-1\leq t\leq 0\\1-t;&0<t\leq 1\\0&{\mbox{otherwise}}\end{cases}}} 時間領域 x [ n ] {\displaystyle x[n]\,} 周波数領域 X ( ω ) {\displaystyle X(\omega )\,} 備考 δ [ n ] {\displaystyle \delta [n]\!} 1 {\displaystyle 1\!} δ [ n − M ] {\displaystyle \delta [n-M]\!} e − i ω M {\displaystyle e^{-i\omega M}\!} M は整数 ∑ m = − ∞ ∞ δ [ n − M m ] {\displaystyle \sum _{m=-\infty }^{\infty }\delta [n-Mm]\,} ∑ m = − ∞ ∞ e − i ω M m = 1 M ∑ k = − ∞ ∞ δ ( ω 2 π − k M ) {\displaystyle \sum _{m=-\infty }^{\infty }e^{-i\omega Mm}={\frac {1}{M}}\sum _{k=-\infty }^{\infty }\delta \left({\frac {\omega }{2\pi }}-{\frac {k}{M}}\right)\,} M は整数 u [ n ] {\displaystyle u[n]\!} 1 1 − e − i ω {\displaystyle {\frac {1}{1-e^{-i\omega }}}\!} e − i a n {\displaystyle e^{-ian}\!} 2 π δ ( ω + a ) {\displaystyle 2\pi \delta (\omega +a)\,} a は実数 cos ( a n ) {\displaystyle \cos(an)\!} π [ δ ( ω − a ) + δ ( ω + a ) ] {\displaystyle \pi \left[\delta (\omega -a)+\delta (\omega +a)\right]} a は実数 sin ( a n ) {\displaystyle \sin(an)\!} π i [ δ ( ω − a ) − δ ( ω + a ) ] {\displaystyle {\frac {\pi }{i}}\left[\delta (\omega -a)-\delta (\omega +a)\right]} a は実数 r e c t [ ( n − M / 2 ) M ] {\displaystyle \mathrm {rect} \left[{(n-M/2) \over M}\right]} sin [ ω ( M + 1 ) / 2 ] sin ( ω / 2 ) e − i ω M / 2 {\displaystyle {\sin[\omega (M+1)/2] \over \sin(\omega /2)}\,e^{-i\omega M/2}} M は整数 sinc [ ( a + n ) ] {\displaystyle \operatorname {sinc} [(a+n)]} e i a ω {\displaystyle e^{ia\omega }\!} a は実数 W ⋅ sinc 2 ( W n ) {\displaystyle W\cdot \operatorname {sinc} ^{2}(Wn)\,} tri ( ω 2 π W ) {\displaystyle \operatorname {tri} \left({\omega \over 2\pi W}\right)} real number W 0 < W ≤ 0.5 {\displaystyle 0<W\leq 0.5} W ⋅ sinc [ W ( n + a ) ] {\displaystyle W\cdot \operatorname {sinc} [W(n+a)]} rect ( ω 2 π W ) ⋅ e j a ω {\displaystyle \operatorname {rect} \left({\omega \over 2\pi W}\right)\cdot e^{ja\omega }} W , a は実数 0 < W ≤ 1 {\displaystyle 0<W\leq 1} { 0 n = 0 ( − 1 ) n n elsewhere {\displaystyle {\begin{cases}0&n=0\\{\frac {(-1)^{n}}{n}}&{\mbox{elsewhere}}\end{cases}}} j ω {\displaystyle j\omega } 微分回路 フィルタとして機能する W ( n + a ) { cos [ π W ( n + a ) ] − sinc [ W ( n + a ) ] } {\displaystyle {\frac {W}{(n+a)}}\left\{\cos[\pi W(n+a)]-\operatorname {sinc} [W(n+a)]\right\}} j ω ⋅ rect ( ω π W ) e j a ω {\displaystyle j\omega \cdot \operatorname {rect} \left({\omega \over \pi W}\right)e^{ja\omega }} W ,a は実数 0 < W ≤ 1 {\displaystyle 0<W\leq 1} 1 π n 2 [ ( − 1 ) n − 1 ] {\displaystyle {\frac {1}{\pi n^{2}}}[(-1)^{n}-1]} | ω | {\displaystyle |\omega |\!} { 0 ; n odd 2 π n ; n even {\displaystyle {\begin{cases}0;&n{\mbox{ odd}}\\{\frac {2}{\pi n}};&n{\mbox{ even}}\end{cases}}} { j ω < 0 0 ω = 0 − j ω > 0 {\displaystyle {\begin{cases}j&\omega <0\\0&\omega =0\\-j&\omega >0\end{cases}}} ヒルベルト変換 C ( A + B ) 2 π ⋅ sinc [ A − B 2 π n ] ⋅ sinc [ A + B 2 π n ] {\displaystyle {\frac {C(A+B)}{2\pi }}\cdot \operatorname {sinc} \left[{\frac {A-B}{2\pi }}n\right]\cdot \operatorname {sinc} \left[{\frac {A+B}{2\pi }}n\right]} A , B は実数 C は複素数
特性 以下の表は、一般的な離散時間フーリエ変換を示したものである。以下のような記法を用いている。
∗ {\displaystyle *\!} 畳み込み を意味する。 x [ n ] ∗ {\displaystyle x[n]^{*}\!} x[n] の複素共役 である。 ρ x y [ n ] {\displaystyle \rho _{xy}[n]\!} x[n] と y[n] の相関 を表す。最初の列は属性の説明、第二列は時間領域での関数表現、第三列は周波数領域でのスペクトル表現である。
特性 時間領域 x [ n ] {\displaystyle x[n]\!} 周波数領域 X ( ω ) {\displaystyle X(\omega )\!} 備考 線形性 a x [ n ] + b y [ n ] {\displaystyle ax[n]+by[n]\!} a X ( e i ω ) + b Y ( e i ω ) {\displaystyle aX(e^{i\omega })+bY(e^{i\omega })\!} 時間におけるシフト x [ n − k ] {\displaystyle x[n-k]\!} X ( e i ω ) e − i ω k {\displaystyle X(e^{i\omega })e^{-i\omega k}\!} k は整数 周波数におけるシフト(変調) x [ n ] e i a n {\displaystyle x[n]e^{ian}\!} X ( e i ( ω − a ) ) {\displaystyle X(e^{i(\omega -a)})\!} a は実数 時間逆転 x [ − n ] {\displaystyle x[-n]\!} X ( e − i ω ) {\displaystyle X(e^{-i\omega })\!} 時間共役 x [ n ] ∗ {\displaystyle x[n]^{*}\!} X ( e − i ω ) ∗ {\displaystyle X(e^{-i\omega })^{*}\!} 時間逆転と共役 x [ − n ] ∗ {\displaystyle x[-n]^{*}\!} X ( e i ω ) ∗ {\displaystyle X(e^{i\omega })^{*}\!} 周波数における微分 n i x [ n ] {\displaystyle {\frac {n}{i}}x[n]\!} d X ( e i ω ) d ω {\displaystyle {\frac {dX(e^{i\omega })}{d\omega }}\!} 周波数における積分 i n x [ n ] {\displaystyle {\frac {i}{n}}x[n]\!} ∫ − π ω X ( e i ϑ ) d ϑ {\displaystyle \int _{-\pi }^{\omega }X(e^{i\vartheta })d\vartheta \!} 時間における畳み込み x [ n ] ∗ y [ n ] {\displaystyle x[n]*y[n]\!} X ( e i ω ) ⋅ Y ( e i ω ) {\displaystyle X(e^{i\omega })\cdot Y(e^{i\omega })\!} 時間における乗算 x [ n ] ⋅ y [ n ] {\displaystyle x[n]\cdot y[n]\!} 1 2 π X ( e i ω ) ∗ Y ( e i ω ) {\displaystyle {\frac {1}{2\pi }}X(e^{i\omega })*Y(e^{i\omega })\!} 相関 ρ x y [ n ] = x [ − n ] ∗ ∗ y [ n ] {\displaystyle \rho _{xy}[n]=x[-n]^{*}*y[n]\!} R x y ( ω ) = X ( e i ω ) ∗ ⋅ Y ( e i ω ) {\displaystyle R_{xy}(\omega )=X(e^{i\omega })^{*}\cdot Y(e^{i\omega })\!}
対称性 フーリエ変換は、実数成分と虚数成分に分離できる。
X ( e i ω ) = X R ( e i ω ) + i X I ( e i ω ) {\displaystyle X(e^{i\omega })=X_{R}(e^{i\omega })+iX_{I}(e^{i\omega })\!}
また、偶数成分と奇数成分に分離できる。
X ( e i ω ) = X E ( e i ω ) + X O ( e i ω ) {\displaystyle X(e^{i\omega })=X_{E}(e^{i\omega })+X_{O}(e^{i\omega })\!}
時間領域 x [ n ] {\displaystyle x[n]\!} 周波数領域 X ( e i ω ) {\displaystyle X(e^{i\omega })\!} x ∗ [ n ] {\displaystyle x^{*}[n]\!} X ∗ ( e − i ω ) {\displaystyle X^{*}(e^{-i\omega })\!} x ∗ [ − n ] {\displaystyle x^{*}[-n]\!} X ∗ ( e i ω ) {\displaystyle X^{*}(e^{i\omega })\!}
参考文献 Alan V. Oppenheim and Ronald W. Schafer (1999年). Discrete-Time Signal Processing (2nd Edition ed.). Prentice Hall Signal Processing Series. ISBN 0-13-754920-2 William McC. Siebert (1986年). Circuits, Signals, and Systems . MIT Electrical Engineering and Computer Science Series. Cambridge, MA: MIT Press Boaz Porat. A Course in Digital Signal Processing . John Wiley and Sons. pp. pp. 27-29 and 104-105. ISBN 0-471-14961-6 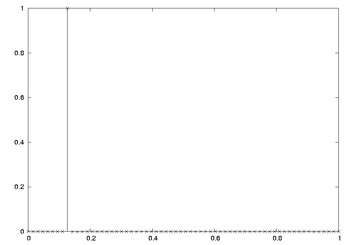

![{\displaystyle x[n],\;n\in \mathbb {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/83b783e3bb4f41250a3bce26399b1885f0e2c975)
![{\displaystyle x[n]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b575dce543a2cf10a5a3e108204b928c2c9aaa54)
![{\displaystyle X(\omega )=\sum _{n=-\infty }^{\infty }x[n]\,e^{-i\omega n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/553acaf0fb714decb09013e12275ca65bed638d7)












![{\displaystyle =\int _{-\infty }^{\infty }\left[T\sum _{n=-\infty }^{\infty }x(nT)\,\delta (t-nT)\right]e^{-i2\pi ft}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b64ca0e4f62aabb30ca99aa7874c5c2bb7dc6462)
![{\displaystyle =\sum _{n=-\infty }^{\infty }T\cdot x(nT)\int _{-\infty }^{\infty }\left[\delta (t-nT)\cdot e^{-i2\pi ft}\right]\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc88e7d8ec21bd8e19fb352a1b315982a6f8f5bb)

![{\displaystyle x[n]=T\cdot x(nT)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d252e6f6bdf6e0dbcb4867d7dbbd257fb24e40a2)














![{\displaystyle \int _{-\infty }^{\infty }X_{T}(f)\cdot e^{i2\pi ft}\,df\ =\ x_{T}(t)\ =\ \sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8db79f90f871af2042bc697018f9f887a25cb432)
![{\displaystyle X(\omega )=\sum _{n=0}^{L-1}x[n]\,e^{-i\omega n}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87ff693d2b4643d2f93625172784c7f92aceb78b)




![{\displaystyle X[k]=X(\omega _{k})=\sum _{n=0}^{L-1}x[n]\,e^{-i2\pi {\frac {k}{N}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07f183a2ac2b666399b9386423ccc27954c5e71f)

![{\displaystyle X[k]=\sum _{n=0}^{N-1}x[n]\,e^{-i2\pi {\frac {k}{N}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b844f108c0b5a787d7b578a4dd2a9814e624b21f)

![{\displaystyle x[n]=0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fff6a735350f46f7b0b92652e1c0e8746d215113)
![{\displaystyle X[k]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c253ca3f48c75b4423d61c78d81e7c2e7c3d29bb)




![{\displaystyle x[n]=e^{i2\pi {\frac {1}{8}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa1e1653bb9fa67bb0158b3a7e9a780d6c08b8db)



![{\displaystyle X(z)=\sum _{n=-\infty }^{\infty }x[n]\,z^{-n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a599aa526823646d32469385b73490b60e28ea7)






![{\displaystyle u[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d2911183bef1ad935d3bc8b5c1be97bac439b7f)


![{\displaystyle \delta [n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1553d02b03c2a79a43f7862ebfb8352705b0b87c)


![{\displaystyle \mathrm {rect} (t)=\sqcap (t)={\begin{cases}0&{\mbox{if }}|t|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}}&{\mbox{if }}|t|={\frac {1}{2}}\\[3pt]1&{\mbox{if }}|t|<{\frac {1}{2}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3585cde90bc1dfbce7b14531690022ad0a7b3a6)



![{\displaystyle \delta [n-M]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dd610c46bdeb2682e719b6a0b445c1cf1893639)

![{\displaystyle \sum _{m=-\infty }^{\infty }\delta [n-Mm]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3ce55d69101c8a851f1b8f09c0492852e8e9e49)





![{\displaystyle \pi \left[\delta (\omega -a)+\delta (\omega +a)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b949fed13f25129a9f8634cb4c0aa34354b0320a)

![{\displaystyle {\frac {\pi }{i}}\left[\delta (\omega -a)-\delta (\omega +a)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b48e8676730fb37bcadaea9b1bb342d107cf2f9)
![{\displaystyle \mathrm {rect} \left[{(n-M/2) \over M}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fa40f5391166dc137b30a45584c1de1a33b2f8c)
![{\displaystyle {\sin[\omega (M+1)/2] \over \sin(\omega /2)}\,e^{-i\omega M/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/883ef01f74f9697fd3a68706785bc6e702c8f961)
![{\displaystyle \operatorname {sinc} [(a+n)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3526652071fa8be34f6bccac88dc94260441a47f)




![{\displaystyle W\cdot \operatorname {sinc} [W(n+a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4185f56193a63b426f87329e9d7c0d1ae50fced)




![{\displaystyle {\frac {W}{(n+a)}}\left\{\cos[\pi W(n+a)]-\operatorname {sinc} [W(n+a)]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7d4cd8e41d9e483f5d90da18cff3661d914ce9b)

![{\displaystyle {\frac {1}{\pi n^{2}}}[(-1)^{n}-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4114640d8ab7e22e07fe380574400fb036941530)



![{\displaystyle {\frac {C(A+B)}{2\pi }}\cdot \operatorname {sinc} \left[{\frac {A-B}{2\pi }}n\right]\cdot \operatorname {sinc} \left[{\frac {A+B}{2\pi }}n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38083aff1d4f22b4848dfafdc988b43142f7c472)

![{\displaystyle x[n]^{*}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e49908fe3dfbd435e478d58b4c10c47e3a609c96)
![{\displaystyle \rho _{xy}[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/358049d59c74edde52765a758324ab97be7ee3a5)
![{\displaystyle x[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91384637c5188ffed9b7929f145a78fb314c4141)

![{\displaystyle ax[n]+by[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c30c8f75093b9bafb5c5bde1392348701ce3be0)

![{\displaystyle x[n-k]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3bfc2b24164de1192ea1e17a90312a3e045911e)

![{\displaystyle x[n]e^{ian}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5f540caf14c269c45b6b5d32ceb555ce8841bae)

![{\displaystyle x[-n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61499a6c6544d338cf6ac340b27ad734c4daba05)


![{\displaystyle x[-n]^{*}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb208f439fc83acd99c3db8d63304b65890993c4)

![{\displaystyle {\frac {n}{i}}x[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2eb71af662480e119b9bd16ff2e4c49151ab4b9)

![{\displaystyle {\frac {i}{n}}x[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/384ec2e6f1fb841111d00c800196000a4d406964)

![{\displaystyle x[n]*y[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e3b1fd5ad225be66dfa022f43a3333b08fb3fb7)

![{\displaystyle x[n]\cdot y[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3e208ac041ff192194184d3c708d7789f9c9178)

![{\displaystyle \rho _{xy}[n]=x[-n]^{*}*y[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d82c9624d4b16650c5652c000d0bb459f794c6)




![{\displaystyle x^{*}[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4793a5489c4d67f5ffcc700e9ba06acd87e231c3)

![{\displaystyle x^{*}[-n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34e0bcbaa111fee79bfcf34b83f9f3b6303ddaed)









