Méthode de meilleure médiane

Les méthodes de meilleure médiane sont des modes de scrutin du type vote par valeurs, où le candidat qui l'emporte est un candidat ayant obtenu la meilleure évaluation médiane. En effet, dans un vote par valeurs, chaque électeur évalue les différents candidats sur une échelle ordonnée, numérique ou verbale.

Les différentes méthodes de meilleure médiane se distinguent par l'échelle de valeur utilisée et par leur traitement des ex aequo, c'est-à-dire par la méthode de classement des candidats ayant obtenu la même évaluation médiane.

Comme tout vote par valeurs, les méthodes de meilleure médiane satisfont à l'indépendance des alternatives non pertinentes et ne tombent pas dans le champ d'application du théorème d'Arrow^[1]. De plus, si l'échelle de valeur est fine, chaque électeur peut exprimer finement son opinion. Les règles de meilleure médiane violent le critère de Condorcet : un candidat peut être élu même si une majorité préfère un autre candidat (et même, en principe, si tous les électeurs sauf un préfèrent un autre candidat^[2].

Définition et notations

Soit ${\displaystyle {\mathcal {C}}}$ l'ensemble des candidats, ${\displaystyle {\mathcal {V}}}$ l'ensemble des électeurs, et ${\displaystyle {\mathcal {G}}}$ un ensemble ordonné fini d'évaluations (par exemple les évaluations "Très bien", "Bien", "Moyen" et "Mauvais").

Pour tout candidat ${\displaystyle c\in {\mathcal {C}}}$, on désigne par ${\displaystyle \alpha _{c}\in {\mathcal {G}}}$ l'évaluation médiane de ${\displaystyle c}$ parmi les évaluations qu'il a reçues des électeurs. Par exemple, s'il y a dix électeurs et que le candidat ${\displaystyle A}$ reçoit trois évaluations "Bien", six évaluations "Moyen" et une évaluation "Mauvais", son évaluation médiane ${\displaystyle \alpha _{A}}$ est "Moyen".

Si, pour tout candidat ${\displaystyle i\neq c}$, ${\displaystyle \alpha _{i}<\alpha _{c}}$, alors ${\displaystyle c}$ obtient une meilleure évaluation médiane que tous les autres candidats, et ${\displaystyle c}$ est élu, quelle que soit la méthode de meilleure médiane retenue.

Lorsque plusieurs candidats ont obtenu la même évaluation médiane, une règle de départage est nécessaire. C'est cette règle de départage qui complète la définition du mode de scrutin, et caractérise les différentes méthodes de meilleure médiane.

Les règles de départage font souvent appel à deux statistiques supplémentaires sur les notes d'un candidat^[3] :

• La part des partisans de ${\displaystyle c}$, notée ${\displaystyle p_{c}}$, qui désigne la part des électeurs attribuant à ${\displaystyle c}$ une évaluation strictement supérieure à sa médiane. Dans l'exemple ci-dessus, les trois évaluations "Bien" sont supérieures à la médiane de ${\displaystyle A}$ ("Moyen"), donc ${\displaystyle p_{A}={\frac {3}{10}}}$.
• La part des opposants à ${\displaystyle c}$, notée ${\displaystyle q_{c}}$, qui désigne la part des électeurs attribuant à ${\displaystyle c}$ une note strictement inférieure à sa médiane. Dans l'exemple ci-dessus, cela correspond à la note "Mauvais", donc ${\displaystyle q_{A}={\frac {1}{10}}}$.

Exemples

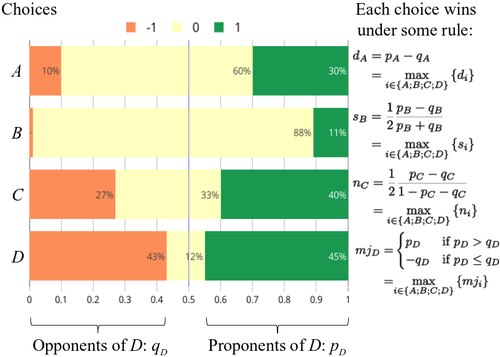
• Le jugement typique ordonne les candidats suivant la plus forte différence entre leur part de partisans et d'opposants, c'est-à-dire suivant la formule : ${\displaystyle d=\alpha +p-q}$ (les indices ${\displaystyle c}$ sont omis par simplicité). Dans l'exemple ci-dessus, et en identifiant l'évaluation "Moyen" avec la note ${\displaystyle 0}$, on a ${\displaystyle d_{A}=0+0.3-0.1=+0.2}$.
• Le jugement usuel ou jugement médian serait la méthode qui offre les meilleures propriétés^[3], mais il ordonne les candidats selon une formule un peu plus complexe : ${\displaystyle n=\alpha +{\frac {1}{2}}{\frac {p-q}{1-p-q}}}$.
• Le jugement central ordonne les candidats selon le plus fort ratio entre les parts de partisans et d'opposants, c'est-à-dire suivant la formule : ${\displaystyle s=\alpha +{\frac {1}{2}}{\frac {p-q}{p+q+\epsilon }}}$ (où ${\displaystyle \epsilon }$ est un nombre arbitrairement petit permettant simplement que le dénominateur reste différent de zéro).
• Le jugement majoritaire s'intéresse au candidat qui est le plus proche d'avoir une autre évaluation que sa médiane et effectue le départage selon cette évaluation. Cela revient à ordonner les candidats suivant leur score ${\displaystyle mj}$^[3], défini par la formule suivante (le symbole ${\displaystyle \mathbf {1} }$ dénote la fonction indicatrice) : ${\displaystyle mj=\alpha +\mathbf {1} _{p>q}p-\mathbf {1} _{p\leq q}q}$.
• Les méthodes de Bucklin (en) se rapprochent des méthodes de meilleure médiane mais ont été développés pour les votes par classement. Elles ordonnent les candidats suivant la formule : ${\displaystyle b=\alpha -q}$. Lors d'un vote par classement, cela revient à compter dans un premier temps les premiers choix des électeurs. Si un candidat est classé en tête par une majorité d'électeurs, ce candidat remporte l'élection. Sinon, les seconds choix sont ajoutés aux premiers choix. Si un candidat obtient la majorité des voix, le vainqueur est le candidat ayant le plus grand nombre de voix accumulées. Les choix inférieurs sont ajoutés si nécessaire.
• Le vote par approbation correspond au cas dégénéré où il n'y a que deux évaluations possibles : l'approbation et la désapprobation. Dans ce cas particulier, toutes les règles de départage sont équivalentes, et le critère de Condorcet est respecté.

Notes et références

Voir aussi

Bibliographie

• (en) Adrien Fabre, « Tie-breaking the Highest Median: Alternatives to the Majority Judgment », Social Choice and Welfare,‎ 2020 (DOI 10.1007/s00355-020-01269-9, lire en ligne)
• Paquet R implémentant différentes méthodes de meilleure médiane, ainsi que la méthode de meilleure somme : HighestMedianRules.

Articles connexes

• Vote par valeurs
• Jugement usuel
• Jugement majoritaire
• Méthodes de Bucklin (en)
• Système électoral
• Critères de systèmes de vote

• Portail des probabilités et de la statistique