Loi de Dulong et Petit

En thermodynamique, la loi de Dulong et Petit est une loi empirique selon laquelle « la capacité thermique isobare molaire ${\displaystyle C_{p}}$ des éléments solides est voisine de ${\displaystyle 3R}$ », soit 25 J K^‑1 mol⁻¹. Pour la plupart des éléments elle est assez bien vérifiée à température ambiante.

Une règle empirique approximative

En 1819 Pierre Louis Dulong et Alexis Thérèse Petit^[1] mesurent la capacité thermique massique ${\displaystyle c_{p}}$ de divers éléments chimiques solides. Les 13 éléments étudiés (S, Fe, Co, Ni, Cu, Zn, Ag, Sn, Te^{[Note 1]}, Pt, Au, Pb, Bi) ont une masse molaire ${\displaystyle M}$ comprise entre 32 et 209 g/mol. Leurs résultats montrent que le produit ${\displaystyle Mc_{p}}$ est indépendant de l'élément considéré^{[Note 2]} et qu'il est égal à 25 J K^‑1 mol⁻¹ (à ± 1 J K^‑1 mol^‑1 près environ). En divisant ce résultat par la constante universelle des gaz parfaits ${\displaystyle R}$ = 8,314 J K^‑1 mol^‑1 et en remplaçant ${\displaystyle Mc_{p}}$ par ${\displaystyle C_{p}}$, capacité calorifique molaire, on en déduit ${\displaystyle C_{p}\simeq 3R}$ ce qui constitue la loi de Dulong et Petit.

Pour les valeurs de ${\displaystyle C_{p}}$ des éléments stables à 298 K (25 °C) voir le lien capacité calorifique. L'indice ${\displaystyle p}$ signifie que les valeurs sont mesurées à pression constante.

Pour les éléments solides^{[Note 3]} on observe que :

• pour la grande majorité des éléments la loi de Dulong et Petit est vérifiée à ± 0,2 ${\displaystyle R}$ près, soit 23 J K⁻¹ mol⁻¹ < ${\displaystyle C_{p}}$ < 27 J K⁻¹ mol⁻¹ environ. Des déviations positives un peu plus élevées sont observées pour quelques métaux alcalins et alcalino-terreux, des terres rares et des actinides ;
• pour le gadolinium (Gd) ${\displaystyle C_{p}}$ atteint 4,45 ${\displaystyle R}$ ;
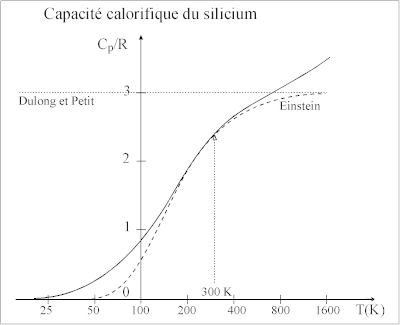
• pour 4 éléments (tableau ci-dessous), dont 3 sont des éléments légers, la valeur de ${\displaystyle C_{p}}$ est inférieure à 3R.

Élément	Be	B	C (graphite)	C (diamant)	Si
${\displaystyle C_{p}/R}$	1,97	1,34	1,02	0,74	2,41

Intérêt historique

Les masses molaires des éléments qui sont gazeux ou qui forment des composés gazeux ont pu être déterminées à l'aide de la loi d'Avogadro^{[Note 4]}.

Les métaux et leurs combinaisons sont généralement solides, ce qui ne permet pas d'utiliser cette loi^[2]. La composition massique d'un composé solide ne donne sa masse molaire qu'à un facteur près. Ainsi, dans la première version du tableau de Mendeleïev en 1869^[3], trois éléments (Ce, In et U) ont été mal placés à cause d'une masse molaire inexacte. Dans le cas de l'oxyde d'uranium le pourcentage en masse de l'oxygène est égal à 11,85 %. À l'époque, la formule supposée de cet oxyde était UO d'où l'on déduit facilement pour l'uranium ${\displaystyle M}$ = 118 g/mol. Or, la valeur de sa capacité calorifique massique est ${\displaystyle c_{p}}$ = 0,116 J K^‑1 g^‑1 ce qui donnerait ${\displaystyle C_{p}=Mc_{p}}$= 13,7 J K^‑1 mol^‑1 = 1,65 ${\displaystyle R}$, valeur en désaccord avec la loi de Dulong et Petit. Par contre, si l'oxyde a pour formule UO₂ alors ${\displaystyle M}$ = 238 g/mol et ${\displaystyle C_{p}}$ = 3,3 ${\displaystyle R}$.

Mendeleïev s'est par la suite appuyé sur les déterminations de c_p pour corriger les valeurs de M de ces trois éléments et les repositionner correctement^[4]. L'extension de la loi de Dulong et Petit aux composés chimiques solides est connue sous le nom de loi de Kopp.

Un modèle moléculaire commun aux gaz et aux solides

On montre en théorie cinétique des gaz que l'énergie d'agitation thermique ${\displaystyle U}$ d'une mole de gaz monoatomique est égale ${\displaystyle 3\,RT/2}$. Le facteur 3 correspond aux trois coordonnées — ou degrés de liberté — nécessaires pour déterminer la position de chaque atome. La capacité calorifique à volume constant ${\displaystyle C_{V}=\mathrm {d} U/\mathrm {d} T}$ est donc égale à ${\displaystyle 3\,R/2}$.

Dans un cristal, chaque atome de masse ${\displaystyle m=M/N_{A}}$ vibre autour de sa position d'équilibre O, sans toutefois la quitter. Son écart par rapport à O est également repérable par 3 coordonnées et son mouvement est celui d'un oscillateur harmonique tridimensionnel. L'énergie moyenne d'un oscillateur harmonique unidimensionnel — ou à un seul degré de liberté — est également partagée entre énergie cinétique et énergie potentielle. En admettant que l'énergie cinétique soit encore égale à ${\displaystyle RT/2,}$ son énergie totale ${\displaystyle U}$ devient égale à ${\displaystyle RT}$, soit encore à ${\displaystyle 3\,RT}$ pour un oscillateur tridimensionnel. En dérivant on en déduit alors une capacité calorifique ${\displaystyle C_{V}}$ à volume constant égale à ${\displaystyle 3\,R}$^{[Note 5]}. On retrouve la loi de Dulong et Petit si l'écart entre ${\displaystyle C_{p}}$ et ${\displaystyle C_{V}}$ est négligeable.

Le modèle d'Einstein

Le modèle précédent ignore la quantification des valeurs de l'énergie de vibration et prévoit que la capacité calorifique est indépendante de ${\displaystyle T}$, ce qui n'est pas le cas. Le modèle d'Einstein tient compte de la quantification de l'énergie.

De façon générale les valeurs de l'énergie d'un atome (niveaux d'énergie) sont quantifiées (discontinues) et peuvent donc être numérotées ${\displaystyle E_{0},E_{1},\dotsc ,E_{i},\dotsc }$. À la température 0 K tous les atomes possèdent la plus basse énergie possible ${\displaystyle E_{0}}$. À la température ${\displaystyle T}$ les atomes se répartissent sur les différents niveaux.

Le nombre ${\displaystyle N_{i}}$ d'atomes d'énergie ${\displaystyle E_{i}}$ constitue la population du niveau ${\displaystyle E_{i}}$. Pour des niveaux simples le rapport ${\displaystyle N_{j}/N_{i}}$ des populations de deux niveaux numérotés ${\displaystyle i}$ et ${\displaystyle j}$ est donné par la loi de distribution de Boltzmann avec ${\displaystyle k={\frac {R}{N_{A}}}}$.

${\displaystyle {\frac {N_{j}}{N_{i}}}=\mathrm {e} ^{-{\frac {E_{j}-E_{i}}{kT}}}}$

Dans cette relation le numérateur ${\displaystyle E_{j}-E_{i}}$ représente l'écart entre deux niveaux que l'on mesure le plus souvent par spectroscopie. Le dénominateur ${\displaystyle kT=RT/N_{A}}$ représente une énergie moyenne d'agitation thermique à l'échelle moléculaire.

Dans le cas d'un oscillateur harmonique quantique, les niveaux sont équidistants. Par conséquent, si l'on prend ${\displaystyle E_{0}=0}$, alors ${\displaystyle E_{v}=vE_{1}}$ où ${\displaystyle v=0,1,2,\dotsc }$ est le nombre quantique de vibration. On pose ${\displaystyle E_{v}=vh\nu }$, où ${\displaystyle \nu }$ est la fréquence de la transition du niveau ${\displaystyle v=0}$ au niveau ${\displaystyle v=1}$ et ${\displaystyle h}$ est la constante de Planck. Le modèle de l'oscillateur harmonique représente les vibrations des molécules diatomiques avec une précision satisfaisante.

Le rapport entre l'espacement des niveaux ${\displaystyle h\nu }$ et l'énergie d'agitation thermique ${\displaystyle kT}$ est noté ${\displaystyle X}$ avec ${\displaystyle X=h\nu /kT}$. La relation de Boltzmann ci-dessus s'écrit ${\displaystyle N_{v}=N_{0}\mathrm {e} ^{-vX}}$.

Deux cas limites sont à considérer :

1. si ${\displaystyle X\gg 1}$ alors ${\displaystyle \mathrm {e} ^{-vX}}$ est égal à 1 pour ${\displaystyle v=0}$ et nul pour ${\displaystyle v>0}$ : le niveau fondamental est le seul peuplé ;
2. si ${\displaystyle X\ll 1}$ alors ${\displaystyle \mathrm {e} ^{-vX}}$ décroît lentement en fonction de ${\displaystyle v}$ et il y a un grand nombre de niveaux peuplés.

Pour aller plus loin, il faut calculer le nombre de particules ${\displaystyle N_{v}}$ sur chaque niveau^[5]. En écrivant que la somme ${\displaystyle \sum N_{v}}$ des populations est égale à ${\displaystyle N_{A}}$ pour 1 mol, on obtient après calcul ${\displaystyle N_{v}=N_{A}(1-\mathrm {e} ^{-X})\mathrm {e} ^{-vX}}$.

L'énergie d'agitation thermique ${\displaystyle U_{\text{vib}}}$ est la somme ${\displaystyle \sum N_{v}E_{v}}$ des énergies des ${\displaystyle N_{A}}$ particules d'où l'on déduit après calcul :

${\displaystyle U_{\text{vib}}=RT{\frac {X}{\mathrm {e} ^{X}-1}}}$

La capacité calorifique de vibration ${\displaystyle C_{\text{vib}}}$ s'en déduit par dérivation par rapport à ${\displaystyle T}$ d'où après calcul :

${\displaystyle C_{\text{vib}}=R{\frac {X^{2}\mathrm {e} ^{X}}{(\mathrm {e} ^{X}-1)^{2}}}}$

Les fonctions représentant ${\displaystyle {\frac {U_{\text{vib}}}{RT}}}$ et ${\displaystyle {\frac {C_{\text{vib}}}{R}}}$ d'un oscillateur harmonique sont appelées 1^re et 2^e d'Einstein. On appelle température d'Einstein le rapport ${\displaystyle \theta _{E}={\frac {h\nu }{k}}}$ si bien que ${\displaystyle X={\frac {h\nu }{kT}}={\frac {\theta _{E}}{T}}}$.

En reprenant les deux cas limite ci-dessus :

1. si ${\displaystyle X\gg 1}$ alors ${\displaystyle U_{\text{vib}}\simeq 0}$ et ${\displaystyle C_{\text{vib}}\simeq 0}$ : c'est ce qu'il se passe pour la plupart des molécules diatomiques gazeuses ;
2. si ${\displaystyle X\ll 1}$ alors ${\displaystyle U_{\text{vib}}\simeq RT}$ et ${\displaystyle C_{\text{vib}}\simeq R}$ comme on le montre facilement après développement limité de ${\displaystyle \mathrm {e} ^{X}}$.

Les atomes d'un solide monoatomique vibrent dans les 3 directions de l'espace donc avec 3 degrés de liberté, et par conséquent ${\displaystyle C_{V}=3\,C_{\text{vib}}}$.

Pour la plupart des éléments solides, et en particulier les métaux courants, la valeur de ${\displaystyle \theta _{E}}$ ne dépasse guère 300 K. Dans ce cas particulier ${\displaystyle \theta _{E}/T=1}$ et on calcule ${\displaystyle C_{\text{vib}}}$ = 0,92 ${\displaystyle R}$ d'où ${\displaystyle C_{V}=3\,C_{\text{vib}}=}$ 2,76 ${\displaystyle R}$. C'est pourquoi, lorsque ${\displaystyle \theta _{E}}$ est inférieure à la température ambiante, ce qui est le plus souvent le cas, la loi de Dulong et Petit est approximativement vérifiée.

Si ${\displaystyle m=M/N_{A}}$ et ${\displaystyle f}$ sont respectivement la masse et la constante de la force de rappel de l'atome, considéré comme un oscillateur harmonique, alors sa fréquence de vibration est donnée par :

${\displaystyle \nu ={\frac {1}{2\pi }}{\sqrt {\frac {f}{m}}}}$

La température d'Einstein ${\displaystyle \theta _{E}={\frac {h\nu }{k}}}$ est proportionnelle à ${\displaystyle \nu }$ donc à ${\displaystyle {\sqrt {\frac {f}{m}}}}$. On trouve donc des valeurs élevées de ${\displaystyle \theta _{E}}$ lorsque le rapport ${\displaystyle {\frac {f}{m}}}$ est grand. Les 4 éléments (Be, B, C, Si) pour lesquels ${\displaystyle C_{p}}$ est très inférieur à ${\displaystyle 3\,R}$ sont des éléments légers et durs (forte valeur de ${\displaystyle f}$). Les valeurs de ${\displaystyle C_{p}}$ augmentent avec ${\displaystyle T}$ et peuvent dépasser largement ${\displaystyle 3\,R}$^[6].

En réalité les vibrations des atomes ne sont pas localisées sur chaque atome mais sont sous forme d'ondes appelées phonons. C'est pourquoi le modèle d'Einstein est grossier et a été remplacé par le modèle de Debye qui donne cependant la même valeur limite ${\displaystyle 3\,R}$ de ${\displaystyle C_{p}}$ à haute température.

Les autres contributions à la capacité calorifique

Contribution de C_p - C_V

Le modèle d'Einstein prévoit que la capacité calorifique ${\displaystyle C_{V}}$ a pour borne supérieure 3R. Mais en fait c'est ${\displaystyle C_{p}}$ que l'on mesure et il dépasse souvent 3R. En thermodynamique, la relation de Mayer générale permet de montrer que ${\displaystyle C_{p}}$ est toujours supérieur à ${\displaystyle C_{V}}$ et que l'écart ${\displaystyle C_{p}-C_{V}}$ est donnée par :

${\displaystyle C_{p}-C_{V}={\frac {\alpha ^{2}VT}{\kappa }}}$

Par conséquent ${\displaystyle C_{p}}$ est toujours supérieur à ${\displaystyle C_{V}}$ . Dans cette relation ${\displaystyle \alpha }$ et ${\displaystyle \kappa }$ sont respectivement les coefficients de dilatation isobare et de compressibilité isotherme.

Par exemple pour le fer à 298 K :

• ${\displaystyle C_{p}}$ = 25,1 J K⁻¹ mol⁻¹ ou 3,02 ${\displaystyle R}$,
• ${\displaystyle \alpha }$ = 3,54 × 10⁻⁵ K⁻¹,
• ${\displaystyle V}$ = 7,12 × 10⁻⁶ m³,
• ${\displaystyle \kappa }$ = 0,59 × 10⁻¹¹ Pa⁻¹.

On en déduit que ${\displaystyle C_{p}-C_{V}}$ = 0,44 J K⁻¹ mol⁻¹ ou 0,05 ${\displaystyle R}$, d'où ${\displaystyle C_{V}}$ = 2,97 ${\displaystyle R}$.

De fait ${\displaystyle C_{p}-C_{V}}$ dépasse rarement 0,1 ${\displaystyle R}$ à quelques exceptions près comme le césium :

• ${\displaystyle C_{p}}$ = 32,2 J K⁻¹ mol⁻¹ ou 3,87 ${\displaystyle R}$,
• ${\displaystyle \alpha }$ = 2,91 × 10⁻⁴ K⁻¹,
• ${\displaystyle V}$ = 68,6 × 10⁻⁴ m³,
• ${\displaystyle \kappa }$ = 0,5 × 10⁻⁹ Pa⁻¹,

d'où ${\displaystyle C_{p}-C_{V}}$ = 3,47 J K⁻¹ mol⁻¹ ou 0,42 ${\displaystyle R}$ et ${\displaystyle C_{V}}$ = 3,45 ${\displaystyle R}$.

Capacité calorifique électronique

En thermodynamique statistique, on montre que les électrons des métaux contribuent assez peu à la capacité calorifique et on la néglige donc dans le modèle d'Einstein.

En fait, cette contribution ${\displaystyle C_{\mathrm {el} }}$ est donnée par :

${\displaystyle C_{\mathrm {el} }=\gamma \;T}$

La constante ${\displaystyle \gamma }$ dépend du métal et elle est le plus souvent de l'ordre de 10⁻³ à 10⁻² J.K⁻¹.mol⁻². Pour Fe^[6] par exemple ${\displaystyle \gamma \simeq \;}$ 5 × 10⁻³ J K⁻² mol⁻¹ d'où ${\displaystyle C_{\mathrm {el} }\simeq \;}$ 1,5 J K⁻¹ mol⁻¹ à 298 K ou encore 0,18R, ce qui représente 6 % du total selon la loi de Dulong et Petit.

Anharmonicité des vibrations

L'anharmonicité des vibrations de grande amplitude et l'apparition de lacunes contribuent aussi à la capacité calorifique en particulier près de la température de fusion^{[Note 6]}.

Transition ferromagnétique

Les métaux ferromagnétiques deviennent paramagnétiques au-dessus de leur température de Curie ${\displaystyle T_{C}}$. La capacité calorifique de ces métaux en fonction de la température augmente progressivement lorsqu'on s'approche de ${\displaystyle T_{C}}$ pour redescendre rapidement ensuite. Ainsi, ${\displaystyle T_{C}}$ = 299 K pour le gadolinium Gd et ${\displaystyle C_{p}}$ = 4,45 R à 298 K. Dans le cas du fer, le ferromagnétisme disparaît à ${\displaystyle T_{C}}$ = 1043 K. Dans cette zone on observe un pic de croissance de ${\displaystyle C_{p}}$ qui dépasse 10R. Il s'agit d'une transition du second ordre^[7]. Par contre, à 1185 K le changement de phase (allotropie) est une transition du premier ordre qui se manifeste par une cassure dans la variation de ${\displaystyle C_{p}}$.

Les capacités calorifiques à basse température

À basse température, de l'ordre de quelques kelvins, on se trouve à l'opposé du domaine d'application de la loi de Dulong et Petit. Le modèle de Debye donne la variation correcte de la capacité calorifique ${\displaystyle C_{p}}$ qui, compte tenu de la contribution électronique ${\displaystyle C_{\mathrm {el} }}$ et du fait que ${\displaystyle C_{p}\approx C_{V}}$, s'écrit ${\displaystyle C_{p}=A\,T^{3}+\gamma T}$.

De cette formule, on déduit ${\displaystyle C_{p}/T=A\,T^{2}+\gamma }$. Par conséquent, en portant ${\displaystyle C_{p}/T}$ en fonction de ${\displaystyle T^{2}}$, on doit obtenir une droite de pente ${\displaystyle A}$ et d'ordonnée à l'origine ${\displaystyle \gamma }$.

La figure montre que pour le fer^[6] ${\displaystyle \gamma }$ = 4,9 × 10⁻³ J K⁻² mol⁻¹.

Notes et références

Notes

Références

• Portail de la physique
• Portail de la chimie