Faserprodukt

Das Faserprodukt (auch Pullback, kartesisches Quadrat oder Pullback-Quadrat) ist ein Begriff aus dem mathematischen Teilgebiet der Kategorientheorie. Zentrale Bedeutung kommt dem Faserprodukt in der algebraischen Geometrie zu.

Der Begriff des Faserproduktes ist dual zum Begriff des Pushout.

Faserprodukt von Mengen

Sind ${\displaystyle \xi \colon X\to S}$ und ${\displaystyle \upsilon \colon Y\to S}$ zwei Abbildungen von Mengen, so ist das Faserprodukt von ${\displaystyle X}$ und ${\displaystyle Y}$ über ${\displaystyle S}$ die Teilmenge

${\displaystyle \{(x,y)\in X\times Y\mid \xi (x)=\upsilon (y)\}}$

des kartesischen Produktes von ${\displaystyle X}$ und ${\displaystyle Y}$.

Faserprodukte in beliebigen Kategorien

Definition über Objekte

Sind Morphismen ${\displaystyle \xi :X\rightarrow S}$ und ${\displaystyle v:Y\rightarrow S}$ in einer Kategorie gegeben, so heißt ein Objekt ${\displaystyle X\times _{S}Y}$ zusammen mit Morphismen

${\displaystyle \mathrm {pr} _{1}\colon X\times _{S}Y\to X}$ und ${\displaystyle \mathrm {pr} _{2}\colon X\times _{S}Y\to Y,}$

den sogenannten kanonischen Projektionen, ein Faserprodukt von ${\displaystyle X}$ und ${\displaystyle Y}$ über ${\displaystyle S}$, wenn ${\displaystyle \xi \circ \mathrm {pr} _{1}=v\circ \mathrm {pr} _{2}}$ und die folgende universelle Eigenschaft erfüllt ist:

Zu jedem Paar von Morphismen ${\displaystyle (f:T\rightarrow X,\,g:T\rightarrow Y)}$ von einem Testobjekt ${\displaystyle T}$ nach ${\displaystyle X}$ bzw. ${\displaystyle Y}$, für das

${\displaystyle \xi f=\upsilon g}$ (als Morphismen ${\displaystyle T\rightarrow S}$)

gilt, gibt es genau einen Morphismus

${\displaystyle c\colon T\to X\times _{S}Y,}$

so dass

${\displaystyle f=\mathrm {pr} _{1}\circ c}$ und ${\displaystyle g=\mathrm {pr} _{2}\circ c}$

gilt.

Anders formuliert: die Funktoren

${\displaystyle \mathrm {Hom} (T,X\times _{S}Y)}$ und ${\displaystyle \mathrm {Hom} (T,X)\times _{\mathrm {Hom} (T,S)}\mathrm {Hom} (T,Y)}$

sind via ${\displaystyle \mathrm {pr} _{1}}$ und ${\displaystyle \mathrm {pr} _{2}}$ natürlich äquivalent.

Definition über Morphismen

Bei einer allgemeineren Herangehensweise werden derartige Paare von Morphismen ${\displaystyle f\operatorname {\colon } T\rightarrow X}$ und ${\displaystyle g\operatorname {\colon } T\rightarrow Y}$ von einem Objekt ${\displaystyle T}$ nach ${\displaystyle X}$ bzw. ${\displaystyle Y}$ als Faserprodukt, Pullback, kartesisches oder Pullback-Quadrat bezeichnet, für die gilt:

1. ${\displaystyle \xi f=\upsilon g}$ (als Morphismen ${\displaystyle T\to S}$)
2. jedes weitere Paar von Morphismen ${\displaystyle f'\operatorname {\colon } T'\rightarrow X}$ und ${\displaystyle g'\operatorname {\colon } T'\rightarrow Y}$ von einem Objekt ${\displaystyle T'}$ nach ${\displaystyle X}$ bzw. ${\displaystyle Y}$, für die ${\displaystyle \xi f'=\upsilon g'}$ gilt, ist über einen eindeutig bestimmten Morphismus ${\displaystyle e\operatorname {\colon } T'\rightarrow T}$ mit dem ersten Paar von Morphismen vertauschbar, d. h. ${\displaystyle g'=ge}$ und ${\displaystyle f'=fe.}$

Die Morphismen von Pullbacks bilden ein kommutatives Diagramm:

${\displaystyle {\begin{array}{rcl}T&{\xrightarrow[{}]{f}}&X\\g\!\downarrow &&\downarrow \!\xi \\Y&{\xrightarrow[{\upsilon }]{}}&S\\\end{array}}}$

Dieses Diagramm stellt einen Kegel über dem Diagramm ${\displaystyle X{\xrightarrow {\xi }}S{\xleftarrow {\upsilon }}Y}$ dar, bei dem der „mittlere“ Pfeil (der zwischen ${\displaystyle T}$ und ${\displaystyle S}$) weggelassen wurde. Die zweite Bedingung drückt aus, dass das Pullback ein Limes aller solchen Kegel ist. Man sagt, ${\displaystyle f}$ entstehe durch Zurückziehen (engl. pull back) von ${\displaystyle \upsilon }$ entlang ${\displaystyle \xi }$ und ${\displaystyle g}$ entstehe durch Zurückziehen von ${\displaystyle \xi }$ entlang ${\displaystyle \upsilon }$ ^[1][2][3]

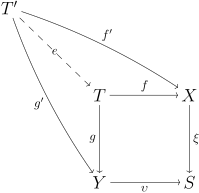
Pullback-Kegel

Gelegentlich werden auch derartige Paare von Morphismen (${\displaystyle f\colon T\to X,g\colon T\to Y}$) von einem Objekt ${\displaystyle T}$ nach ${\displaystyle X}$ bzw. ${\displaystyle Y}$, für die lediglich

${\displaystyle \xi f=\upsilon g}$ (als Morphismen ${\displaystyle T\to S}$)

gilt, als Pullback-Kegel bezeichnet; Morphismen von Pullback-Kegeln sind über entsprechende kommutative Diagramme definiert. Das Faserprodukt ist dann ein Endobjekt der Kategorie der möglichen Pullback-Kegel über dem Diagramm ${\displaystyle X{\xrightarrow {\xi }}S{\xleftarrow {\upsilon }}Y.}$^[4][5]

Eindeutigkeit

Die Komponenten ${\displaystyle T,f}$ und ${\displaystyle g}$ des Faserproduktes aus der Definition über Morphismen müssen nicht eindeutig bestimmt sein, sind aber eindeutig bis auf Isomorphie. D. h., ist ${\displaystyle T'}$ zusammen mit Abbildungen ${\displaystyle f'}$ und ${\displaystyle g'}$ ein weiteres derartiges Faserprodukt, so sind ${\displaystyle T}$ und ${\displaystyle T'}$ isomorph und ${\displaystyle f'}$ und ${\displaystyle g'}$ eindeutig durch ${\displaystyle f}$ und ${\displaystyle g}$ bestimmt. Für ein und dasselbe Objekt ${\displaystyle T}$ kann es ebenfalls verschiedene Möglichkeiten für die Morphismen ${\displaystyle f}$ und ${\displaystyle g}$ geben. Die verschiedenen Varianten sind dann aber wiederum durch einen Isomorphismus (von ${\displaystyle T}$ auf sich selbst) eindeutig durch einander bestimmt.

Auch ${\displaystyle X\times _{S}Y}$ aus der Definition über Objekte ist im Allgemeinen nur ein Symbol für mehrere mögliche, jeweils zueinander isomorphe Objekte. Es wird jedoch gewöhnlich eine Standarddarstellung für ${\displaystyle X\times _{S}Y}$ angegeben; z. B. in der Kategorie der Mengen die Menge:

${\displaystyle D=\{(x,y)|x\in X,y\in Y\ \mathrm {und} \ \xi (x)=\upsilon (y)\}\cong X\times _{S}Y}$^[1]

Bezeichnung

Die Bezeichnungen werden nicht ganz einheitlich verwendet. Gemeinhin wird in mathematischen Texten mit Faserprodukt eher das sich ergebende Objekt der Produktbildung bezeichnet, während mit Pullback das sich ergebende Paar von Abbildungen bezeichnet wird. Hinzu kommt noch die verallgemeinerte Bezeichnung des Faserproduktes als Produkt über …. Mit kartesisches oder Pullback-Quadrat wird dann auch eher die Gesamtkonstruktion oder das Pullback-Diagramm bezeichnet. Letztlich werden die Bezeichnungen jedoch synonym gedeutet und werden nur unterschiedlich eingesetzt, um jeweils einen bestimmten Aspekt des Faserproduktes ins Zentrum der Betrachtung zu rücken.^[6][7][8]

Eigenschaften

• Ist ${\displaystyle X\to Y}$ ein beliebiger Morphismus, so ist

${\displaystyle X\times _{Y}Y\cong X}$.

• Sind ${\displaystyle \xi }$ und ${\displaystyle \upsilon }$ injektive Mengenabbildungen (allgemein Monomorphismen), so ist das Faserprodukt der Schnitt (der Bilder) von ${\displaystyle X}$ und ${\displaystyle Y}$
• Ist ${\displaystyle S}$ eine einelementige Menge, so ist das Faserprodukt isomorph zum kartesischen Produkt. Die Standarddarstellung (s. o.) des Faserproduktes in der Kategorie der Mengen ist dann identisch mit dem kartesischen Produkt. Ist allgemein ${\displaystyle S}$ ein Endobjekt, so ist das Faserprodukt isomorph zum allgemeinen kategoriellen Produkt.
• Die Standarddarstellung (s. o.) des Faserproduktes in der Kategorie der Mengen ist eine Untermenge des kartesischen Produktes. Allgemein gibt es stets einen Monomorphismus vom Faserprodukt in das allgemeine kategorielle Produkt

${\displaystyle X\times _{S}Y\to X\times Y}$

(falls beide Konstruktionen existieren).

• Für eine asymmetrische Sichtweise des Faserproduktes siehe Basiswechsel (Faserprodukt).

Beispiele

• Das Faserprodukt ist ein spezieller Limes. Aufgrund der Stetigkeit des jeweiligen Vergissfunktors ist in den folgenden Kategorien – deren Objekten stets Mengen zugrunde liegen – die zugrunde liegende Menge des Faserproduktes (in dieser Kategorie) gleich dem Faserprodukt (in der Kategorie der Mengen) der zugrunde liegenden Mengen:

Gruppen, abelsche Gruppen, Ringe, Moduln, Vektorräume, topologische Räume, Banachräume.

• In der Kategorie der Schemata ist das Faserprodukt lokal durch Tensorprodukte gegeben. Es ist i. A. nicht das Faserprodukt der zugrundeliegenden topologischen Räume!
• Der Gleichheitsverbund in der relationalen Algebra.

Faserprodukte in der algebraischen Geometrie

Die obige kategorielle Definition wird insbesondere in der algebraischen Geometrie benutzt, um das Faserprodukt ${\displaystyle X\times _{S}Y}$ zweier Schemata mit gegebenen Morphismen ${\displaystyle \xi \colon X\to S,\nu \colon Y\to S}$ zu definieren.

Wenn ${\displaystyle X,Y}$ und ${\displaystyle S}$ affine Schemata sind, dann ist auch ${\displaystyle X\times _{S}Y}$ ein affines Schema.^[9] Aus ${\displaystyle X=Spec(A),Y=Spec(B),S=Spec(R)}$ folgt nämlich

${\displaystyle X\times _{S}Y=Spec(A\otimes _{R}B)}$.^[10]

Dies gibt eine explizite Beschreibung (und beweist insbesondere die Existenz) des Faserprodukts affiner Schemata.

Eine explizite Beschreibung für Faserprodukte beliebiger Schemata erhält man wie folgt. Sei ${\displaystyle \textstyle S=\bigcup _{i}U_{i}}$ eine Überdeckung durch affine Schemata, und für alle ${\displaystyle i}$ seien

${\displaystyle \xi ^{-1}(U_{i})=\bigcup _{j}V_{ij},\nu ^{-1}(U_{i})=\bigcup _{k}W_{ik}}$

jeweils Überdeckungen durch affine Schemata, dann ist

${\displaystyle X\times _{S}Y=\bigcup _{i}\bigcup _{j,k}V_{ij}\times _{U_{i}}W_{ik}}$

eine Überdeckung durch affine Schemata, insbesondere ist damit ${\displaystyle X\times _{S}Y}$ als Schema definiert.^[11]

Für einen Punkt ${\displaystyle x}$ eines Schemas bezeichne jeweils ${\displaystyle \kappa (x)}$ den zugehörigen lokalen Ring. Die Punkte des Faserprodukts ${\displaystyle X\times _{S}Y}$ entsprechen dann bijektiv den Tupeln ${\displaystyle (x,y,s,{\mathfrak {p}})}$ mit ${\displaystyle \xi (x)=\nu (y)=s}$ und einem Primideal ${\displaystyle {\mathfrak {p}}\subset \kappa (x)\otimes _{\kappa (s)}\kappa (y)}$.^[12]

Einzelnachweise

1. ↑ ^{a b} R. Goldblatt u. a.: Topoi – The Categorial Analysis of Logic. Studies in Logic and the Foundations of Mathematics. Vol. 98. North-Holland Publishing Company, Amsterdam / New York / Oxford 1979, ISBN 0-444-85207-7, Kap. 3.13, S. 63 (englisch, Beschreibung von Pullbacks.). 
2. ↑ R. Goldblatt u. a.: Topoi – The Categorial Analysis of Logic. Studies in Logic and the Foundations of Mathematics. Vol. 98. North-Holland Publishing Company, Amsterdam / New York / Oxford 1979, ISBN 0-444-85207-7, Kap. 3.11, S. 58 (englisch, Beschreibung von Limites und Co-Limites.). 
3. ↑ Hartmut Ehrig, Michael Pfender und Studenten der Mathematik: Kategorien und Automaten. Walter de Gruyter, Berlin / New York 1972, ISBN 3-11-003902-8, Def. 3.34, S. 60 (Definition von Pullbacks.). 
4. ↑ R. Goldblatt u. a.: Topoi – The Categorial Analysis of Logic. Studies in Logic and the Foundations of Mathematics. Vol. 98. North-Holland Publishing Company, Amsterdam / New York / Oxford 1979, ISBN 0-444-85207-7, Kap. 3.6, S. 44 (englisch, Definition von Endobjekten.). 
5. ↑ Hartmut Ehrig, Michael Pfender und Studenten der Mathematik: Kategorien und Automaten. Walter de Gruyter, Berlin / New York 1972, ISBN 3-11-003902-8, Def. 1.25, S. 19 (Definition von Endobjekten.). 
6. ↑ R. Goldblatt u. a.: Topoi – The Categorial Analysis of Logic. Studies in Logic and the Foundations of Mathematics. Vol. 98. North-Holland Publishing Company, Amsterdam / New York / Oxford 1979, ISBN 0-444-85207-7 (englisch). 
7. ↑ Hartmut Ehrig, Michael Pfender und Studenten der Mathematik: Kategorien und Automaten. Walter de Gruyter, Berlin / New York 1972, ISBN 3-11-003902-8. 
8. ↑ Saunders Mac Lane: Kategorien. Begriffssprache und mathematische Theorie. Springer-Verlag, Berlin / Heidelberg / New York 1972, ISBN 3-540-05634-3 (amerikanisches Englisch: Categories. For the Working Mathematician. Übersetzt von Klaus Schürger). 
9. ↑ The Stacks Project Lemma 25.17.3
10. ↑ The Stacks Project Lemma 25.6.7
11. ↑ The Stacks Project Lemma 25.17.4
12. ↑ The Stacks Project Lemma 25.17.5