Mètode d'Euler

En matemàtiques i ciència computacional, el mètode d'Euler és un procés numèric per a resoldre equacions diferencials ordinàries (EDOs) amb un valor inicial donat. És el cas més bàsic de mètode explícit d'integració numèrica per a equacions diferencials ordinàries.^[1] El mètode pren el nom de l'autor, Leonhard Euler.^[2]

Descripció geomètrica informal

Considerem el problema de trobar una corba desconeguda que comença en un punt donat i satisfà una equació diferencial donada. L'equació diferencial es pot interpretar com una fórmula que permet calcular el pendent de la recta tangent a qualsevol punt de la corba, a partir de la posició d'aquest punt.

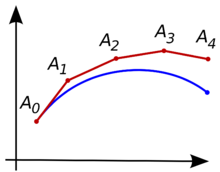
La idea és que, encara que la corba és inicialment desconeguda, el seu punt inicial, que notarem per ${\displaystyle A_{0},}$ és conegut (vegeu la il·lustració superior). Llavors, a partir de l'equació diferencial, es pot calcular el pendent de la corba a ${\displaystyle A_{0}}$, i per tant, la recta tangent en el punt inicial.

Avancem un petit pas al llarg d'aquesta recta tangent cap a un punt ${\displaystyle A_{1}.}$ Si suposem que ${\displaystyle A_{1}}$ encara es troba sobre la corba, es pot utilitzar el mateix raonament que pel punt ${\displaystyle A_{0}}$. Després d'alguns passos, es calcula la corba poligonal ${\displaystyle A_{0}A_{1}A_{2}A_{3}\dots }$. En general, aquesta corba no divergeix gaire de la corba original desconeguda, i l'error entre totes dues corbes es pot reduir si la mida del pas és prou petita i l'interval de computació és finit.^[3]

Derivació

Volem aproximar la solució del problema de valor inicial:

${\displaystyle y'(t)=f(t,y(t)),\qquad \qquad y(t_{0})=y_{0},}$

utilitzant els dos primers termes de la sèrie de Taylor de y, que representa l'aproximació lineal al voltant del punt (t₀,y(t₀)). Un pas del mètode d'Euler des de t_n cap a t_n+1 = t_n + h és^[4]

${\displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n}).}$^[2]

El mètode d'Euler és explícit, és a dir, la solució ${\displaystyle y_{n+1}}$ és una funció explícita de ${\displaystyle y_{i}}$ per ${\displaystyle i\leq n}$.

Encara que el mètode d'Euler integra una EDO de primer ordre, qualsevol EDO d'ordre ${\displaystyle N}$ es pot representar com una EDO de primer ordre amb més d'una variable introduint ${\displaystyle N-1}$ variables addicionals, ${\displaystyle y'}$, ${\displaystyle y''}$, ..., ${\displaystyle y^{(N)}}$, i formulant ${\displaystyle N}$ equacions de primer grau amb aquestes noves variables.^[5] El mètode d'Euler es pot aplicar al vector ${\displaystyle \mathbf {y} (t)=(y(t),y'(t),y''(t),...,y^{(N)}(t))}$ per integrar el sistema d'ordre més elevat.^[3]

Error

La magnitud dels errors generats pel mètode d'Euler es pot demostrar per comparació amb una sèrie de Taylor de y.^[3] Si assumim que ${\displaystyle f(t)}$ i ${\displaystyle y(t)}$ es coneixen exactament al temps ${\displaystyle t_{0},}$ llavors el mètode d'Euler dona la solució aproximada al temps ${\displaystyle t_{0}+h}$ com:

${\displaystyle y(t_{0}+h)=y(t_{0})+hf(t_{0},y(t_{0}))=y(t_{0})+hy'(t_{0})\,\qquad \qquad }$

(la segona igualtat prové que y satisfà l'equació diferencial ${\displaystyle y'=f(t,y)}$). En comparació, la sèrie de Taylor a ${\displaystyle h}$ sobre ${\displaystyle t_{0}}$ dona:

${\displaystyle y(t_{0}+h)=y(t_{0})+hy'(t_{0})+{\frac {1}{2}}h^{2}y''(t_{0})+O(h^{3}).}$^[6]

L'error introduït pel mètode d'Euler ve donat per la diferència entre aquestes equacions:

${\displaystyle {\frac {1}{2}}h^{2}y''(t_{0})+O(h^{3}).}$

Per ${\displaystyle h}$ petita, l'error dominant per pas és proporcional a ${\displaystyle h^{2}}$. Per resoldre el problema sobre un rang donat de ${\displaystyle t}$, el nombre de passos necessaris és proporcional a ${\displaystyle 1/h}$, per tant s'espera que l'error total al final del temps fixat sigui proporcional a ${\displaystyle h}$ (error per pas multiplicat pel nombre de passos). Per aquesta raó, es diu que el mètode d'Euler és de primer ordre.^[2] Això fa que el mètode d'Euler sigui menys precís (per petites ${\displaystyle h}$) que altres tècniques d'ordres més alts com els mètodes de Runge-Kutta.

El mètode d'Euler també pot ser numèricament inestable. Aquesta limitació, juntament amb la seva lentitud en la convergència, fa que el mètode d'Euler no sigui gaire utilitzat, excepte com a exemple simple d'integració numèrica.^[7]

Referències